Z przebiegu geometrii i matematyki uczniowie są przyzwyczajeni do tego, że pojęcie pochodnej jest im przekazywane poprzez obszar figury, różniczki, granice funkcji, a także granice. Spróbujmy spojrzeć na pojęcie pochodnej pod innym kątem i ustalić, w jaki sposób można powiązać pochodną z funkcją trygonometryczną.
Rozważmy więc dowolną krzywą opisaną przez funkcję abstrakcyjną y = f(x).
Wyobraźmy sobie, że rozkład jazdy jest mapą trasy turystycznej. Przyrost ∆x (delta x) na rysunku oznacza pewną odległość ścieżki, a ∆y oznacza zmianę wysokości ścieżki nad poziomem morza.
Następnie okazuje się, że stosunek ∆x/∆y będzie charakteryzował złożoność trasy na każdym jej odcinku. Znając tę wartość, możesz śmiało stwierdzić, czy podejście/zejście jest strome, czy potrzebny będzie sprzęt wspinaczkowy i czy turyści potrzebują określonego treningu fizycznego. Ale ten wskaźnik będzie ważny tylko dla jednego małego przedziału ∆x.
Jeżeli organizator wycieczki przyjmie wartości dla punktów początkowego i końcowego szlaku, czyli ∆x jest równe długości trasy, to nie będzie mógł uzyskać obiektywnych danych o stopniu trudności podróży. Dlatego konieczne jest skonstruowanie kolejnego wykresu, który będzie charakteryzował prędkość i „jakość” zmian na ścieżce, czyli innymi słowy wyznaczy stosunek ∆x/∆y dla każdego „metru” trasy.
Wykres ten będzie wizualną pochodną określonej ścieżki i obiektywnie opisuje jej zmiany w każdym interesującym nas przedziale. Bardzo łatwo to sprawdzić; wartość ∆x/∆y jest niczym innym jak różnicą przyjętą dla określonej wartości x i y. Zastosujmy różniczkowanie nie do konkretnych współrzędnych, ale do funkcji jako całości:

Funkcje pochodne i trygonometryczne
Funkcje trygonometryczne są nierozerwalnie związane z pochodnymi. Można to zrozumieć z następny rysunek. Rysunek osi współrzędnych przedstawia funkcję Y = f (x) - niebieska krzywa.
K (x0; f (x0)) to dowolny punkt, x0 + ∆x to przyrost wzdłuż osi OX, a f (x0 + ∆x) to przyrost wzdłuż osi OY w pewnym punkcie L.

Narysujmy linię prostą przechodzącą przez punkty K i L i skonstruujmy prawy trójkąt KLN. Jeśli przesuniesz w myślach odcinek LN wzdłuż wykresu Y = f (x), wówczas punkty L i N będą dążyć do wartości K (x0; f (x0)). Nazwijmy ten punkt warunkowym początkiem wykresu – granicą, ale jeśli funkcja jest nieskończona, przynajmniej na jednym z przedziałów, to pragnienie to również będzie nieskończone, a jej wartość graniczna blisko 0.
Naturę tej tendencji można opisać styczną do wybranego punktu y = kx + b lub wykresem pochodnej pierwotnej funkcji dy – zielonej prostej.
Ale gdzie tu jest trygonometria?! Wszystko jest bardzo proste, rozważ trójkąt prostokątny KLN. Wartość różnicowa dla konkretny punkt K jest tangensem kąta α lub ∠K:

W ten sposób możemy opisać znaczenie geometryczne pochodnej i jej związek z funkcjami trygonometrycznymi.
Wzory pochodne na funkcje trygonometryczne
Należy zapamiętać przekształcenia sinusa, cosinusa, tangensa i cotangensa przy wyznaczaniu pochodnej.

Dwa ostatnie wzory nie są błędem, chodzi o to, że istnieje różnica pomiędzy określeniem pochodnej prostego argumentu a funkcją o tym samym charakterze.
Rozważmy tabela porównawcza ze wzorami na pochodne sinusa, cosinusa, tangensa i cotangensa:

Wyprowadzono także wzory na pochodne arcsine, arccosinus, arcustangens i arccotangens, chociaż są one używane niezwykle rzadko:

Warto zauważyć, że powyższe wzory wyraźnie nie wystarczą do pomyślnego rozwiązania typowych zadań USE, co zostanie wykazane przy rozwiązywaniu konkretnego przykładu znajdowania pochodnej wyrażenia trygonometrycznego.
Ćwiczenia: Należy znaleźć pochodną funkcji i znaleźć jej wartość dla π/4:

Rozwiązanie: Aby znaleźć y’, należy przypomnieć sobie podstawowe wzory na przekształcenie funkcji pierwotnej na pochodną, a mianowicie.
Temat:„Pochodna funkcji trygonometrycznych”.
Typ lekcji– lekcja utrwalania wiedzy.
Formularz lekcji– lekcja zintegrowana.
Miejsce lekcji w systemie lekcji dla tej sekcji- lekcja ogólna.
Cele stawiane są kompleksowo:
- edukacyjny: zna zasady różniczkowania, potrafi zastosować zasady obliczania pochodnych przy rozwiązywaniu równań i nierówności; doskonalenie przedmiotu, w tym umiejętności obliczeniowych i zdolności; umiejętności obsługi komputera;
- rozwijanie: rozwój umiejętności intelektualnych i logicznych oraz zainteresowań poznawczych;
- edukacyjny: kultywuj zdolność przystosowania się do nowoczesne warunki szkolenie.
Metody:
- reprodukcyjny i produktywny;
- praktyczne i werbalne;
- niezależna praca;
- zaprogramowane uczenie się, T.S.O.;
- połączenie frontu, grupy i praca indywidualna;
- zróżnicowane uczenie się;
- indukcyjno-dedukcyjne.
Formy kontroli:
- ankieta ustna,
- sterowanie programowane,
- niezależna praca,
- indywidualne zadania na komputerze,
- recenzja koleżeńska z wykorzystaniem karty diagnostycznej studenta.
POSTĘP LEKCJI
I. Moment organizacyjny
II. Aktualizacja wiedzy referencyjnej
a) Komunikowanie celów i założeń:
- zna zasady różniczkowania, potrafi zastosować zasady obliczania pochodnych przy rozwiązywaniu problemów, równań i nierówności;
- doskonalenie przedmiotu, w tym umiejętności obliczeniowych i zdolności; umiejętności obsługi komputera;
- rozwijać umiejętności intelektualne i logiczne oraz zainteresowania poznawcze;
- kultywować zdolność przystosowania się do współczesnych warunków uczenia się.
b) Powtórzenie materiału edukacyjnego
Zasady obliczania pochodnych (powtarzanie wzorów na komputerze z dźwiękiem). dok.7.
- Jaka jest pochodna sinusa?
- Jaka jest pochodna cosinusa?
- Jaka jest pochodna tangensa?
- Jaka jest pochodna kotangensu?
III. Praca ustna
Znajdź pochodną. |
|||
Opcja 1. |
Opcja 2. |
||
Na = 2X + 5. |
Na = 2X – 5. |
||
Na= 4cos X. |
Na= 3 grzech X. |
||
Na= tg X+ctg X. |
Na= tg X-ctg X. |
||
Na= grzech 3 X. |
Na= cos 4 X. |
||
Opcje odpowiedzi. |
|||
– 4 grzech X |
– 3kos X |
||
1/co2 X+ 1/grzech 2 X |
1/co2 X–1/grzech 2 X |
1/grzech 2 X–1/cos 2 X |
|
– 4sin4 X |
– 3cos3 X |
||
Wymień notesy. W kartach diagnostycznych zadania wykonane poprawnie oznaczaj znakiem +, a zadania wykonane błędnie znakiem –.
IV. Rozwiązywanie równań za pomocą pochodnej
– Jak znaleźć punkty, w których pochodna wynosi zero?
Aby znaleźć punkty, w których pochodna tę funkcję równa się zero, potrzebujesz:
– określić charakter funkcji,
– znajdź obszar definicje funkcji,
– znajdź pochodną tej funkcji,
– rozwiązać równanie F "(X) = 0,
– wybierz poprawną odpowiedź.
Zadanie 1.
Dany: Na
= X-grzech X.
Znajdować: punkty, w których pochodna wynosi zero.
Rozwiązanie. Funkcja jest zdefiniowana i różniczkowalna na zbiorze wszystkich liczb rzeczywistych, ponieważ funkcje są określone i różniczkowalne na zbiorze wszystkich liczb rzeczywistych G(X) = X I T(X) = – grzech X.
Korzystając z reguł różniczkowania, otrzymujemy F
"(X) = (X-grzech X)" = (X)” – (grzech X)” = 1 – sałata X.
Jeśli F "(X) = 0, wtedy 1 – cos X = 0.
sałata X= 1/; pozbądźmy się irracjonalności w mianowniku, otrzymamy cos X
= /2.
Według formuły T= ± arcco A+ 2n, n Z, otrzymujemy: X= ± arccos /2 + 2n, n Z.
Odpowiedź: x = ± /4 + 2n, n Z.
V. Rozwiązywanie równań za pomocą algorytmu
Znajdź, w jakich punktach pochodna zanika.
F(X) = grzech X+bo X |
F(X) = grzech 2 X – X |
F(X) = 2X+cos(4 X – ) |
Uczeń może wybrać jeden z trzech przykładów. Pierwszy przykład ma ocenę „ 3 ", drugi - " 4 „, trzeci -” 5 " Rozwiązanie w zeszytach, a następnie wzajemne sprawdzenie. Decyzję podejmuje jeden uczeń na tablicy. Jeśli rozwiązanie okaże się błędne, uczeń musi wrócić do algorytmu i spróbować rozwiązać jeszcze raz.
Zaprogramowane sterowanie.
Opcja 1 |
Opcja 2 |
|||
y = 2X 3 |
y = 3X 2 |
|||
y = 1/4 X 4 + 2X 2 – 7 |
y = 1/2 X 4 + 4X + 5 |
|||
y = X 3 + 4X 2
– 3X. |
y = 2X 3 – 9X 2
+ 12X + 7. |
|||
y= grzech 2 X– co 3 X. |
y= cos 2 X– grzech 3 X. |
|||
y= tg X–ctg( X + /4). |
y=ctg X+ tg( X – /4). |
|||
y= grzech 2 X. |
y= cos 2 X. |
|||
Opcje odpowiedzi. |
||||
|
Aby znaleźć pochodna funkcji trygonometrycznej trzeba użyć tabela instrumentów pochodnych, czyli pochodne 6-13. Kiedy znajdziesz pochodne prostych funkcji trygonometrycznych Aby uniknąć typowych błędów, należy zwrócić uwagę na następujące punkty:
Przykład 1. Znajdź pochodną funkcji Rozwiązanie. powiedzmy z pochodna cosinusa wszystko jest jasne, powie wielu, którzy zaczynają studiować instrumenty pochodne. Co byś powiedział na pochodna sinusa dwanaście podzielone przez pi? Odpowiedź: liczyć równy zeru! Tutaj sinus (w końcu funkcja!) jest pułapką, ponieważ argumentem nie jest zmienna X ani żadna inna zmienna, ale po prostu liczba. Oznacza to, że sinus tej liczby jest również liczbą. A pochodna liczby (stała), jak wiemy z tabeli pochodnych, jest równa zeru. Zostawiamy więc tylko minus sinus X i znajdujemy jego pochodną, nie zapominając o znaku:
Przykład 2. Znajdź pochodną funkcji
Rozwiązanie. Drugi wyraz jest taki sam jak pierwszy wyraz w poprzednim przykładzie. Oznacza to, że jest to liczba, a pochodna tej liczby wynosi zero. Pochodną drugiego wyrazu znajdujemy jako pochodną ilorazu:
Przykład 3. Znajdź pochodną funkcji Rozwiązanie. To jest kolejny problem: tutaj w pierwszym członie nie ma arcsinusa ani innej funkcji trygonometrycznej, ale jest x, czyli jest to funkcja od x. Dlatego różniczkujemy go jako wyraz w sumie funkcji:
Tutaj wymagana była umiejętność operacji na ułamkach, a mianowicie eliminowania trzypiętrowej struktury ułamka. Przykład 4. Znajdź pochodną funkcji
Rozwiązanie. Tutaj litera „phi” pełni tę samą rolę, co „x” w poprzednich przypadkach (iw większości innych, ale nie wszystkich) - zmienna niezależna. Dlatego też, szukając pochodnej iloczynu funkcji, nie będziemy się spieszyć z deklaracją pochodnej pierwiastka z „phi” równej zero. Więc:
Ale to nie koniec rozwiązań. Ponieważ podobne terminy ujęto w dwa nawiasy, nadal musimy przekształcić (uprościć) wyrażenie. Dlatego mnożymy nawiasy przez czynniki za nimi stojące, a następnie sprowadzamy wyrazy do wspólnego mianownika i wykonujemy inne elementarne przekształcenia:
Przykład 5. Znajdź pochodną funkcji Rozwiązanie. W tym przykładzie będziemy musieli poznać fakt, że istnieje taka funkcja trygonometryczna – sieczna – i jej wzory poprzez cosinus. Rozróżnijmy:
Przykład 6. Znajdź pochodną funkcji
Rozwiązanie. W tym przykładzie będziemy musieli zapamiętać ze szkoły wzór na podwójny kąt. Ale najpierw rozróżnijmy:
(to jest wzór na podwójny kąt) Przedstawiono pochodne odwrotnych funkcji trygonometrycznych oraz wyprowadzenie ich wzorów. Podano także wyrażenia na pochodne wyższego rzędu. Linki do stron z bardziej szczegółowym opisem wyprowadzania wzorów. Najpierw wyprowadzamy wzór na pochodną arcsinusa. Pozwalać Znaleźliśmy więc: A poprzednia formuła ma postać: Stąd Dokładnie w ten sposób można otrzymać wzór na pochodną arcus cosinus. Łatwiej jest jednak zastosować wzór odnoszący się do odwrotnych funkcji trygonometrycznych: Następnie Bardziej szczegółowy opis znajduje się na stronie „Wyprowadzanie pochodnych arcsinusa i arccosinusa”. Tam jest to podanewyprowadzanie instrumentów pochodnych na dwa sposoby - omówiono powyżej i zgodnie ze wzorem na pochodną funkcji odwrotnej. Arcus tangens jest odwrotną funkcją tangensa: Różniczkuj ze względu na zmienną x:- omówiono powyżej i zgodnie ze wzorem na pochodną funkcji odwrotnej. Stąd dostajemy równanie różniczkowe, co spełniają pochodne arcsine pierwszego i drugiego rzędu: Różniczkując to równanie, możemy znaleźć pochodne wyższego rzędu.: Tutaj . Wielomian spełnia równanie różniczkowe:Pochodna arccosinusa n-tego rzędu Zatem pochodne tych funkcji różnią się jedynie znakiem:Pochodne arcustangens Pozwalać . Znaleziono pochodną cotangensu łuku pierwszego rzędu: Oto jednostka urojona, . Różniczkujemy raz i sprowadzamy ułamek do wspólnego mianownika: Podstawiając , otrzymujemy:Pochodna arcustangens n-tego rzędu Zatem pochodną arcustangens n-tego rzędu można przedstawić na kilka sposobów:Pochodne cotangensu łuku Zastosujmy wzór łączący odwrotne funkcje trygonometryczne: Wtedy pochodna n-tego rzędu stycznej łuku różni się jedynie znakiem od pochodnej stycznej łuku: Wykorzystana literatura: X N.M. Gunther, RO Kuźmin, Zbiór problemów matematyki wyższej, „Lan”, 2003. X Wyprowadzając pierwszy wzór tabeli, zaczniemy od definicji funkcji pochodnej w punkcie. Weźmy gdzie – dowolna liczba rzeczywista, tj. – dowolna liczba z dziedziny definicji funkcji. Zapiszmy granicę stosunku przyrostu funkcji do przyrostu argumentu w punkcie: Należy zauważyć, że pod znakiem granicznym uzyskuje się wyrażenie, które nie jest niepewnością zera podzieloną przez zero, ponieważ licznik nie zawiera wartości nieskończenie małej, ale dokładnie zero. Innymi słowy, przyrost funkcji stałej wynosi zawsze zero.Zatem,. pochodna funkcji stałejjest równa zeru w całym obszarze definicji P – dowolna liczba rzeczywista. Najpierw udowodnijmy wzór na wykładnik naturalny, czyli dla p = 1, 2, 3, … Będziemy korzystać z definicji pochodnej. Zapiszmy granicę stosunku przyrostu funkcji potęgowej do przyrostu argumentu: Aby uprościć wyrażenie w liczniku, zwracamy się do wzoru dwumianu Newtona: Stąd,Dowodzi to wzoru na pochodną funkcji potęgowej dla wykładnika naturalnego. Pochodna funkcji wykładniczej. Przedstawiamy wyprowadzenie wzoru na pochodną w oparciu o definicję: Jeśli przypomnimy sobie drugą niezwykłą granicę, dochodzimy do wzoru na pochodną funkcji wykładniczej: Pochodna funkcji logarytmicznej.Udowodnijmy dla wszystkich wzór na pochodną funkcji logarytmicznej X z dziedziny definicji i wszystkich ważnych wartości podstawy A logarytm Z definicji pochodnej mamy: Jak zauważyłeś, w trakcie dowodu przekształcenia przeprowadzono wykorzystując własności logarytmu. Równość Pochodne funkcji trygonometrycznych.Aby wyprowadzić wzory na pochodne funkcji trygonometrycznych, będziemy musieli przypomnieć sobie niektóre wzory trygonometryczne, a także pierwszą niezwykłą granicę. Z definicji pochodnej funkcji sinus mamy Skorzystajmy ze wzoru na różnicę sinusów: Pozostaje przejść do pierwszego niezwykłego ograniczenia: Zatem pochodna funkcji grzech x Jest bo x. Wzór na pochodną cosinusa dowodzi się dokładnie w ten sam sposób. Zatem pochodna funkcji bo x Jest –grzech x. Wzory na tablicę pochodnych na tangens i cotangens wyprowadzimy korzystając ze sprawdzonych zasad różniczkowania (pochodna ułamka). Pochodne funkcji hiperbolicznych.Reguły różniczkowania oraz wzór na pochodną funkcji wykładniczej z tabeli pochodnych pozwalają nam wyprowadzić wzory na pochodne sinusa, cosinusa hiperbolicznego, tangensa i kotangensa. Pochodna funkcji odwrotnej.Aby uniknąć zamieszania podczas prezentacji, oznaczmy w indeksie dolnym argument funkcji, za pomocą której dokonuje się różniczkowania, czyli jest to pochodna funkcji k(x) Przez X. Teraz sformułujmy zasada znajdowania pochodnej funkcji odwrotnej. Niech funkcje y = f(x) I x = g(y) wzajemnie odwrotne, określone odpowiednio na przedziałach i. Jeśli w punkcie istnieje skończona niezerowa pochodna funkcji k(x), to w tym punkcie istnieje skończona pochodna funkcji odwrotnej g(y), I Zasadę tę można przeformułować dla dowolnego X z przedziału , to otrzymujemy Sprawdźmy zasadność tych formuł. Znajdźmy funkcję odwrotną logarytmu naturalnego Widzimy to z tabeli instrumentów pochodnych Upewnijmy się, że wzory na znalezienie pochodnych funkcji odwrotnej prowadzą nas do tych samych wyników: | ||||


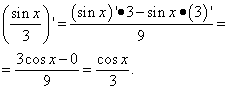
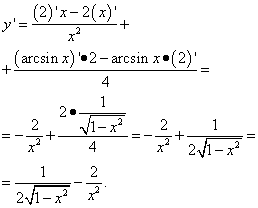

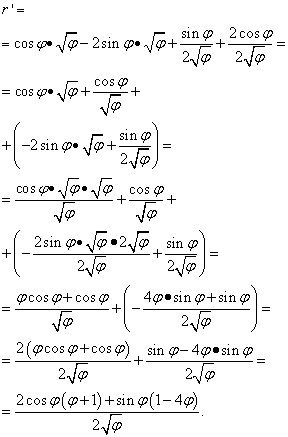








 jest prawdziwe ze względu na drugą niezwykłą granicę.
jest prawdziwe ze względu na drugą niezwykłą granicę.




 .
.



