Edukacyjny:
- Wspieranie aktywności;
Typ lekcji
Sprzęt:
- Projektor i komputer.
Plan lekcji
1. Moment organizacyjny
2. Aktualizowanie wiedzy
4. Wykonanie testu
5. Rozwiązanie ćwiczeń
6. Podsumowanie lekcji
7. Praca domowa.
Postęp lekcji
1. Moment organizacyjny
Dzisiaj będziemy kontynuować pracę nad mnożeniem i dzieleniem liczb dodatnich i ujemnych. Zadaniem każdego z Was jest odgadnięcie, jak opanował ten temat i w razie potrzeby doprecyzowanie tego, co jeszcze nie do końca wyszło. Ponadto dowiecie się wielu ciekawych rzeczy na temat pierwszego miesiąca wiosny – marca. (Slajd 1)
2. Aktualizowanie wiedzy.
3x=27; -5x=-45; x:(2,5)=5.
3. Dyktando matematyczne(slajd 6.7)
Opcja 1
Opcja 2
4. Wykonanie testu ( slajd 8)
Odpowiedź : Martius
5.Rozwiązanie ćwiczeń
(Slajdy od 10 do 19)
4 marca -
2) y×(-2,5)=-15
6 marca
3) -50, 4:x=-4, 2
4) -0,25:5×(-260)
13 marca
5) -29,12: (-2,08)
14 marca
6) (-6-3,6×2,5) ×(-1)
7) -81,6:48×(-10)
17 marca
8) 7,15×(-4): (-1,3)
22 marca
9) -12,5×50: (-25)
10) 100+(-2,1:0,03)
30 marca
6. Podsumowanie lekcji
7. Praca domowa:
Wyświetl zawartość dokumentu
„Mnożenie i dzielenie liczb o różnych znakach”
Temat lekcji: „Mnożenie i dzielenie liczb za pomocą różne znaki”.
Cele lekcji: powtórzenie przestudiowanego materiału na temat „Mnożenie i dzielenie liczb o różnych znakach”, ćwiczenie umiejętności stosowania operacji mnożenia i dzielenia liczby dodatniej przez liczbę ujemną i odwrotnie, a także liczby ujemnej przez liczbę liczba ujemna.
Cele lekcji:
Edukacyjny:
Ujednolicenie przepisów w tym temacie;
Kształtowanie umiejętności i umiejętności pracy z operacjami mnożenia i dzielenia liczb o różnych znakach.
Edukacyjny:
Rozwój zainteresowań poznawczych;
Rozwój logiczne myślenie, pamięć, uwaga;
Edukacyjny:
Wspieranie aktywności;
Zaszczepienie w uczniach umiejętności samodzielnej pracy;
Rozbudzanie miłości do natury, zaszczepianie zainteresowania znakami ludowymi.
Typ lekcji. Powtórzenie lekcji i uogólnienie.
Sprzęt:
Projektor i komputer.
Plan lekcji
1. Moment organizacyjny
2. Aktualizowanie wiedzy
3. Dyktando matematyczne
4. Wykonanie testu
5. Rozwiązanie ćwiczeń
6. Podsumowanie lekcji
7. Praca domowa.
Postęp lekcji
1. Moment organizacyjny
Witam chłopaki! Co robiliśmy na poprzednich lekcjach? (Mnożenie i dzielenie liczby wymierne.)
Dzisiaj będziemy kontynuować pracę nad mnożeniem i dzieleniem liczb dodatnich i ujemnych. Zadaniem każdego z Was jest odgadnięcie, jak opanował ten temat i w razie potrzeby doprecyzowanie tego, co jeszcze nie do końca wyszło. Ponadto dowiecie się wielu ciekawych rzeczy na temat pierwszego miesiąca wiosny – marca. (Slajd 1)
2. Aktualizowanie wiedzy.
Zapoznaj się z zasadami mnożenia i dzielenia liczb dodatnich i ujemnych.
Zapamiętaj zasadę mnemoniczną. (slajd 2)
Wykonaj mnożenie: (slajd 3)
5x3; 9×(-4); -10×(-8); 36×(-0,1); -20×0,5; -13×(-0,2).
2. Wykonaj dzielenie: (slajd 4)
48:(-8); -24: (-2); -200:4; -4,9:7; -8,4: (-7); 15:(- 0,3).
3. Rozwiąż równanie: (slajd 5)
3x=27; -5x=-45; x:(2,5)=5.
3. Dyktando matematyczne(slajd 6.7)
Opcja 1
Opcja 2
Uczniowie wymieniają się zeszytami, rozwiązują test i wystawiają ocenę.
4. Wykonanie testu ( slajd 8)
Dawno, dawno temu na Rusi liczyło się lata od 1 marca, od początku rolniczej wiosny, od pierwszego wiosenne krople. Marzec był „rozpoczęciem” roku. Nazwa miesiąca „marzec” pochodzi od Rzymian. Nazwali ten miesiąc imieniem jednego ze swoich bogów. Test pomoże ci dowiedzieć się, jaki to bóg.
Odpowiedź : Martius
Rzymianie nazwali jeden miesiąc w roku Martiusem na cześć boga wojny Marsa. Na Rusi nazwa ta została uproszczona poprzez wzięcie tylko czterech pierwszych liter (slajd 9).
Ludzie mówią: „Marzec jest niewierny, czasem płacze, czasem się śmieje”. Z marcem wiąże się wiele znaków ludowych. Niektóre z jego dni mają swoje własne nazwy. Stwórzmy teraz wszyscy razem ludową księgę miesiąca marca.
5.Rozwiązanie ćwiczeń
Uczniowie przy tablicy rozwiązują przykłady, których odpowiedzią są dni miesiąca. Na tablicy pojawia się przykład, a następnie dzień miesiąca z nazwą i znak ludowy.
(Slajdy od 10 do 19)
4 marca - Arkhipa. Na Arkhip kobiety miały spędzać cały dzień w kuchni. Im więcej jedzenia przygotuje, tym bogatszy będzie dom.
2) y×(-2,5)=-15
6 marca- Timofey-wiosna. Jeśli w dzień Timofeya będzie śnieg, żniwa przyjdą na wiosnę.
3) -50, 4:x=-4, 2
4) -0,25:5×(-260)
13 marca- Wasilij kroplownik: kapie z dachów. Ptaki gniazdują, a ptaki wędrowne przylatują z ciepłych miejsc.
5) -29,12: (-2,08)
14 marca- Evdokia (Avdotya the Ivy) - śnieg spłaszcza się pod wpływem naparu. Drugie spotkanie wiosenne (pierwsze na Spotkaniu). Jaka jest Evdokia, takie jest lato. Evdokia jest czerwona - a wiosna jest czerwona; śnieg na Evdokii - na żniwa.
6) (-6-3,6×2,5) ×(-1)
7) -81,6:48×(-10)
17 marca- Gerasim, rooker, przyniósł gawrony. Gawrony lądują na gruntach ornych, a jeśli polecą prosto do swoich gniazd, czeka ich przyjazna wiosna.
8) 7,15×(-4): (-1,3)
22 marca- Sroki - dzień równa się nocy. Zima się kończy, zaczyna wiosna, przybywają skowronki. Przez stary zwyczaj Z ciasta piecze się skowronki i brodziki.
9) -12,5×50: (-25)
10) 100+(-2,1:0,03)
30 marca- Aleksiejowi jest ciepło. Woda pochodzi z gór, a ryby z obozu (z zimowej chaty). Niezależnie od tego, jakie są tego dnia strumienie (duże czy małe), takie jest również równina zalewowa (powódź).
6. Podsumowanie lekcji
Chłopaki, podobała Wam się dzisiejsza lekcja? Czego nowego się dzisiaj nauczyłeś? Co powtórzyliśmy? Proponuję przygotować własny księgozbiór na kwiecień. Trzeba znaleźć znaki kwietnia i stworzyć przykłady z odpowiedziami odpowiadającymi dniowi miesiąca.
7. Praca domowa: s. 218 nr 1174, 1179(1) (Slajd20)
W tym artykule zajmiemy się mnożenie liczb o różnych znakach. Tutaj najpierw sformułowamy zasadę mnożenia liczb dodatnich i ujemnych, uzasadnimy ją, a następnie rozważymy zastosowanie tej reguły przy rozwiązywaniu przykładów.
Nawigacja strony.
Zasada mnożenia liczb o różnych znakach
Mnożenie liczby dodatniej przez liczbę ujemną, a także liczby ujemnej przez liczbę dodatnią, przeprowadza się w następujący sposób: zasada mnożenia liczb o różnych znakach: aby pomnożyć liczby o różnych znakach, należy pomnożyć i umieścić znak minus przed otrzymanym iloczynem.
Zapiszmy to tę zasadę w formie listu. Dla każdej dodatniej liczby rzeczywistej a i dowolnej ujemnej liczby rzeczywistej −b równość a·(−b)=−(|a|·|b|) , a także dla liczby ujemnej −a i liczby dodatniej b równość (−a)·b=−(|a|·|b|) .
Zasada mnożenia liczb o różnych znakach jest w pełni zgodna właściwości operacji na liczbach rzeczywistych. Rzeczywiście na ich podstawie łatwo wykazać, że dla liczb rzeczywistych i dodatnich a i b istnieje łańcuch równości postaci a·(−b)+a·b=a·((−b)+b)=a·0=0, co dowodzi, że a·(−b) i a·b są liczbami przeciwnymi, co implikuje równość a·(−b)=−(a·b) . Z tego wynika ważność omawianej reguły mnożenia.
Należy zauważyć, że podana zasada mnożenia liczb o różnych znakach obowiązuje zarówno w przypadku liczb rzeczywistych, jak i wymiernych oraz liczb całkowitych. Wynika to z faktu, że operacje na liczbach wymiernych i całkowitych mają te same własności, które zostały użyte w powyższym dowodzie.
Oczywiste jest, że mnożenie liczb o różnych znakach zgodnie z otrzymaną regułą sprowadza się do mnożenia liczb dodatnich.
Pozostaje tylko rozważyć przykłady zastosowania zdemontowanej reguły mnożenia przy mnożeniu liczb o różnych znakach.
Przykłady mnożenia liczb o różnych znakach
Przyjrzyjmy się kilku rozwiązaniom przykłady mnożenia liczb przez różne znaki. Zacznijmy od prostego przypadku, aby skupić się na etapach reguły, a nie na złożoności obliczeniowej.
Przykład.
Pomnóż liczbę ujemną −4 przez liczbę dodatnią 5.
Rozwiązanie.
Zgodnie z zasadą mnożenia liczb o różnych znakach, najpierw musimy pomnożyć wartości bezwzględne pierwotnych czynników. Moduł -4 wynosi 4, a moduł 5 wynosi 5, a pomnożenie liczb naturalnych 4 i 5 daje 20. Na koniec pozostaje postawić znak minus przed wynikową liczbą, mamy -20. To kończy mnożenie.
W skrócie rozwiązanie można zapisać w następujący sposób: (−4)·5=−(4,5)=−20.
Odpowiedź:
(−4)·5=−20.
Mnożąc ułamki zwykłe o różnych znakach, musisz umieć mnożyć ułamki zwykłe, mnożyć ułamki dziesiętne i ich kombinacje z liczbami naturalnymi i mieszanymi.
Przykład.
Mnoży liczby o różnych znakach 0, (2) i .
Rozwiązanie.
Zamieniając okresowy ułamek dziesiętny na ułamek zwykły, a także zamieniając liczbę mieszaną na ułamek niewłaściwy, z iloczynu pierwotnego  dojdziemy do produktu zwykłe ułamki z różnymi znakami formy. Iloczyn ten, zgodnie z zasadą mnożenia liczb o różnych znakach, jest równy . Pozostaje tylko pomnożyć ułamki zwykłe w nawiasach
dojdziemy do produktu zwykłe ułamki z różnymi znakami formy. Iloczyn ten, zgodnie z zasadą mnożenia liczb o różnych znakach, jest równy . Pozostaje tylko pomnożyć ułamki zwykłe w nawiasach  .
.
Ta lekcja dotyczy mnożenia i dzielenia liczb wymiernych.
Treść lekcjiMnożenie liczb wymiernych
Zasady mnożenia liczb całkowitych dotyczą także liczb wymiernych. Innymi słowy, aby pomnożyć liczby wymierne, trzeba to umieć
Trzeba także znać podstawowe prawa mnożenia, takie jak: prawo przemienności mnożenia, prawo łączenia mnożenia, prawo rozdzielności mnożenia i mnożenia przez zero.
Przykład 1. Znajdź wartość wyrażenia
Jest to mnożenie liczb wymiernych o różnych znakach. Aby pomnożyć liczby wymierne o różnych znakach, należy pomnożyć ich moduły i postawić minus przed wynikową odpowiedzią.
Aby wyraźnie zobaczyć, że mamy do czynienia z liczbami o różnych znakach, każdą liczbę wymierną ujęliśmy w nawiasy kwadratowe wraz z jej znakami

Moduł liczby jest równy , a moduł liczby jest równy . Po pomnożeniu powstałych modułów jako ułamków dodatnich otrzymaliśmy odpowiedź, ale przed odpowiedzią stawiamy minus, zgodnie z wymaganą przez nas regułą. Aby zapewnić ten minus przed odpowiedzią, w nawiasach wykonano mnożenie modułów, poprzedzone minusem.
Krótkie rozwiązanie wygląda następująco:
![]()
Przykład 2. Znajdź wartość wyrażenia 


Przykład 3. Znajdź wartość wyrażenia 
Jest to mnożenie ujemnych liczb wymiernych. Aby pomnożyć ujemne liczby wymierne, należy pomnożyć ich moduły i umieścić plus przed wynikową odpowiedzią
Rozwiązanie tego przykładu można krótko zapisać:

Przykład 4. Znajdź wartość wyrażenia 
Rozwiązanie tego przykładu można krótko zapisać:

Przykład 5. Znajdź wartość wyrażenia
Jest to mnożenie liczb wymiernych o różnych znakach. Pomnóżmy moduły tych liczb i postawmy minus przed wynikową odpowiedzią

Krótkie rozwiązanie będzie wyglądać znacznie prościej:
Przykład 6. Znajdź wartość wyrażenia
Zamieńmy liczbę mieszaną na ułamek niewłaściwy. Przepiszmy resztę tak, jak jest
Otrzymaliśmy mnożenie liczb wymiernych o różnych znakach. Pomnóżmy moduły tych liczb i postawmy minus przed wynikową odpowiedzią. Wpis z modułami można pominąć, aby nie zaśmiecać wyrażenia
Rozwiązanie tego przykładu można krótko napisać
Przykład 7. Znajdź wartość wyrażenia
Jest to mnożenie liczb wymiernych o różnych znakach. Pomnóżmy moduły tych liczb i postawmy minus przed wynikową odpowiedzią

Początkowo odpowiedź okazała się ułamkiem niewłaściwym, ale podkreśliliśmy w niej całą część. Należy zauważyć, że część całkowita została oddzielona od modułu ułamkowego. Otrzymaną liczbę mieszaną ujęto w nawiasy poprzedzone znakiem minus. Ma to na celu zapewnienie spełnienia wymogu reguły. A zasada wymagała, aby otrzymaną odpowiedź poprzedzić minusem.
Rozwiązanie tego przykładu można krótko zapisać:
Przykład 8. Znajdź wartość wyrażenia 
Najpierw pomnóżmy i pomnóżmy wynikową liczbę przez pozostałą liczbę 5. Pomińmy wpis z modułami, żeby nie zaśmiecać wyrażenia.
Odpowiedź: wartość wyrażenia  równa się -2.
równa się -2.
Przykład 9. Znajdź znaczenie wyrażenia: 
Zamieńmy liczby mieszane na ułamki niewłaściwe:

Otrzymaliśmy mnożenie ujemnych liczb wymiernych. Pomnóżmy moduły tych liczb i postawmy plus przed wynikową odpowiedzią. Wpis z modułami można pominąć, aby nie zaśmiecać wyrażenia
Przykład 10. Znajdź wartość wyrażenia
Wyrażenie składa się z kilku czynników. Zgodnie z prawem skojarzeniowym mnożenia, jeśli wyrażenie składa się z kilku czynników, wówczas iloczyn nie będzie zależał od kolejności działań. Dzięki temu możemy ocenić dane wyrażenie w dowolnej kolejności.
Nie wymyślajmy koła na nowo, ale obliczmy to wyrażenie od lewej do prawej, w kolejności czynników. Pomińmy wpis z modułami, żeby nie zaśmiecać wyrażenia
Trzecia akcja:
Czwarta akcja:
Odpowiedź: wartość wyrażenia wynosi
Przykład 11. Znajdź wartość wyrażenia
Pamiętajmy o prawie mnożenia przez zero. Prawo to stanowi, że iloczyn jest równy zeru, jeśli co najmniej jeden z czynników równy zeru.
W naszym przykładzie jeden z czynników jest równy zero, więc nie tracąc czasu odpowiadamy, że wartość wyrażenia jest równa zero:

Przykład 12. Znajdź wartość wyrażenia 
Iloczyn jest równy zero, jeśli przynajmniej jeden z czynników jest równy zero.
W naszym przykładzie jeden z czynników jest równy zero, więc nie tracąc czasu odpowiadamy, że wartość wyrażenia  równa się zeru:
równa się zeru:

Przykład 13. Znajdź wartość wyrażenia 
Możesz zastosować kolejność działań i najpierw obliczyć wyrażenie w nawiasach, a wynikową odpowiedź pomnożyć przez ułamek.
Możesz także skorzystać z rozdzielnego prawa mnożenia - pomnóż każdy wyraz sumy przez ułamek i dodaj otrzymane wyniki. Będziemy korzystać z tej metody.

Zgodnie z kolejnością działań, jeśli wyrażenie zawiera dodawanie i mnożenie, najpierw należy wykonać mnożenie. Dlatego w powstałym nowym wyrażeniu umieśćmy w nawiasach te parametry, które należy pomnożyć. W ten sposób możemy wyraźnie zobaczyć, które działania wykonać wcześniej, a które później:
Trzecia akcja:
![]()
Odpowiedź: wartość wyrażenia  równa się
równa się
Rozwiązanie tego przykładu można zapisać znacznie krócej. Będzie to wyglądać tak:
Oczywiste jest, że ten przykład można rozwiązać nawet w umyśle. Dlatego powinieneś rozwinąć umiejętność analizowania wyrażeń przed ich rozwiązaniem. Prawdopodobnie da się to rozwiązać mentalnie i zaoszczędzić mnóstwo czasu i nerwów. A na sprawdzianach i egzaminach, jak wiadomo, czas jest bardzo cenny.
Przykład 14. Znajdź wartość wyrażenia −4,2 × 3,2
Jest to mnożenie liczb wymiernych o różnych znakach. Pomnóżmy moduły tych liczb i postawmy minus przed wynikową odpowiedzią

Zwróć uwagę, jak pomnożono moduły liczb wymiernych. W w tym przypadku aby pomnożyć moduły liczb wymiernych, potrzeba było .
Przykład 15. Znajdź wartość wyrażenia −0,15 × 4
Jest to mnożenie liczb wymiernych o różnych znakach. Pomnóżmy moduły tych liczb i postawmy minus przed wynikową odpowiedzią

Zwróć uwagę, jak pomnożono moduły liczb wymiernych. W tym przypadku, aby pomnożyć moduły liczb wymiernych, trzeba było to umieć.
Przykład 16. Znajdź wartość wyrażenia −4,2 × (−7,5)
Jest to mnożenie ujemnych liczb wymiernych. Pomnóżmy moduły tych liczb i postawmy plus przed wynikową odpowiedzią
Podział liczb wymiernych
Zasady dzielenia liczb całkowitych dotyczą także liczb wymiernych. Innymi słowy, aby móc dzielić liczby wymierne, trzeba to umieć
W przeciwnym razie stosuje się te same metody dzielenia ułamków zwykłych i dziesiętnych. Aby podzielić ułamek zwykły przez inny ułamek, należy pomnożyć pierwszy ułamek przez odwrotność drugiego ułamka.
I dzielić dziesiętny na inny ułamek dziesiętny, należy przesunąć przecinek w dzielnej i dzielniku w prawo o tyle cyfr, ile jest po przecinku w dzielniku, a następnie wykonać dzielenie jak zwykłą liczbę.
Przykład 1. Znajdź znaczenie wyrażenia:
Jest to dzielenie liczb wymiernych o różnych znakach. Aby obliczyć takie wyrażenie, należy pomnożyć pierwszy ułamek przez odwrotność drugiego.
Zatem pomnóżmy pierwszy ułamek przez odwrotność drugiego.
Otrzymaliśmy mnożenie liczb wymiernych o różnych znakach. Wiemy już, jak obliczyć takie wyrażenia. Aby to zrobić, musisz pomnożyć moduły tych liczb wymiernych i postawić minus przed wynikową odpowiedzią.
Dokończmy ten przykład do końca. Wpis z modułami można pominąć, aby nie zaśmiecać wyrażenia
Zatem wartość wyrażenia wynosi
Szczegółowe rozwiązanie wygląda następująco:
Krótkie rozwiązanie wyglądałoby tak:
Przykład 2. Znajdź wartość wyrażenia
Jest to dzielenie liczb wymiernych o różnych znakach. Aby obliczyć to wyrażenie, należy pomnożyć pierwszy ułamek przez odwrotność drugiego.
Odwrotnością drugiego ułamka jest ułamek . Pomnóżmy przez to pierwszy ułamek:

Krótkie rozwiązanie wyglądałoby tak:
Przykład 3. Znajdź wartość wyrażenia
Jest to dzielenie ujemnych liczb wymiernych. Aby obliczyć to wyrażenie, musisz ponownie pomnożyć pierwszy ułamek przez odwrotność drugiego.
Odwrotnością drugiego ułamka jest ułamek . Pomnóżmy przez to pierwszy ułamek:

Otrzymaliśmy mnożenie ujemnych liczb wymiernych. Wiemy już, jak obliczane jest takie wyrażenie. Musisz pomnożyć moduły liczb wymiernych i umieścić plus przed wynikową odpowiedzią.
Zakończmy ten przykład do końca. Możesz pominąć wpis z modułami, aby nie zaśmiecać wyrażenia:
Przykład 4. Znajdź wartość wyrażenia
Aby obliczyć to wyrażenie, należy pomnożyć pierwszą liczbę −3 przez ułamek odwrotny .
Odwrotnością ułamka jest ułamek . Pomnóż przez nią pierwszą liczbę −3
Przykład 6. Znajdź wartość wyrażenia
Aby obliczyć to wyrażenie, musisz pomnożyć pierwszy ułamek przez odwrotność 4.
Odwrotnością liczby 4 jest ułamek. Pomnóż przez to pierwszy ułamek
Przykład 5. Znajdź wartość wyrażenia
Aby obliczyć to wyrażenie, należy pomnożyć pierwszy ułamek przez odwrotność −3
Odwrotność -3 jest ułamkiem. Pomnóżmy przez to pierwszy ułamek:
Przykład 6. Znajdź wartość wyrażenia -14,4: 1,8
Jest to dzielenie liczb wymiernych o różnych znakach. Aby obliczyć to wyrażenie, należy podzielić moduł dywidendy przez moduł dzielnika i postawić minus przed wynikową odpowiedzią.

Zwróć uwagę, jak moduł dzielnej został podzielony przez moduł dzielnika. W tym przypadku, żeby zrobić to poprawnie, trzeba było umieć.
Jeśli nie chcesz bawić się z ułamkami dziesiętnymi (a to się często zdarza), to przelicz te liczby mieszane na ułamki niewłaściwe, a następnie wykonaj dzielenie.
Obliczmy w ten sposób poprzednie wyrażenie −14,4: 1,8. Zamieńmy ułamki dziesiętne na liczby mieszane:
![]()
Zamieńmy teraz powstałe liczby mieszane na ułamki niewłaściwe:

![]()
Teraz możesz dzielić bezpośrednio, czyli dzielić ułamek przez ułamek. Aby to zrobić, musisz pomnożyć pierwszy ułamek przez odwrotny ułamek drugiego:

Przykład 7. Znajdź wartość wyrażenia 
Zamieńmy ułamek dziesiętny −2,06 na ułamek niewłaściwy i pomnóżmy ten ułamek przez odwrotność drugiego ułamka:

Ułamki wielopiętrowe
Często można spotkać się z wyrażeniem, w którym dzielenie ułamków zapisuje się za pomocą linii ułamkowej. Na przykład wyrażenie można zapisać w następujący sposób:
Jaka jest różnica między wyrażeniami i ? Naprawdę nie ma różnicy. Te dwa wyrażenia mają to samo znaczenie i możemy postawić między nimi znak równości:

W pierwszym przypadku znakiem podziału jest dwukropek, a wyrażenie zapisywane jest w jednym wierszu. W drugim przypadku dzielenie ułamków zapisuje się za pomocą linii ułamkowej. Rezultatem jest ułamek, na który ludzie zgadzają się zadzwonić wielopoziomowy.
W przypadku takich wyrażeń wielopiętrowych należy zastosować te same zasady dzielenia ułamków zwykłych. Pierwszy ułamek należy pomnożyć przez odwrotność drugiego.
Używanie takich ułamków w roztworze jest niezwykle niewygodne, dlatego można je zapisać w zrozumiałej formie, używając dwukropka zamiast linii ułamkowej jako znaku dzielenia.
Na przykład napiszmy ułamek wielopiętrowy w zrozumiałej formie. Aby to zrobić, musisz najpierw dowiedzieć się, gdzie jest pierwszy ułamek, a gdzie drugi, ponieważ nie zawsze można to zrobić poprawnie. Ułamki wielopoziomowe mają kilka linii ułamkowych, które mogą być mylące. Główna linia ułamkowa oddzielająca pierwszy ułamek od drugiego jest zwykle dłuższa od pozostałych.
Po określeniu głównej linii ułamkowej możesz łatwo zrozumieć, gdzie jest pierwszy ułamek, a gdzie drugi:

Przykład 2.
Znajdujemy główną linię ułamkową (jest najdłuższa) i widzimy, że liczba całkowita −3 jest dzielona przez ułamek zwykły
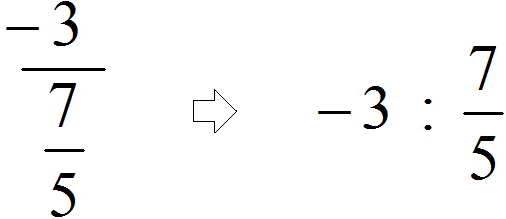
A gdybyśmy błędnie przyjęli za wiodącą drugą prostą ułamkową (tą krótszą), to okazałoby się, że dzielimy ułamek przez liczbę całkowitą 5. W tym przypadku, nawet jeśli to wyrażenie zostanie poprawnie obliczone, to problem zostanie rozwiązany niepoprawnie, ponieważ dywidenda w tym przypadku W tym przypadku liczba wynosi -3, a dzielnikiem jest ułamek .
Przykład 3. Zapiszmy ułamek wielopoziomowy w zrozumiałej formie
Znajdujemy główną linię ułamkową (jest najdłuższa) i widzimy, że ułamek jest dzielony przez liczbę całkowitą 2

A jeśli błędnie przyjmiemy jako wiodącą pierwszą linię ułamkową (tą krótszą), to okaże się, że dzielimy liczbę całkowitą -5 przez ułamek. W tym przypadku, nawet jeśli to wyrażenie zostanie poprawnie obliczone, problem zostanie rozwiązany niepoprawnie, ponieważ dywidenda w tym przypadku ułamek wynosi , a dzielnik jest liczbą całkowitą 2.
Pomimo tego, że ułamki wielopoziomowe są niewygodne w obsłudze, spotkamy się z nimi bardzo często, szczególnie podczas studiowania matematyki wyższej.
Naturalnie przełożenie wielopiętrowego ułamka na zrozumiałą formę wymaga dodatkowego czasu i miejsca. Dlatego możesz użyć więcej szybka metoda. Ta metoda jest wygodna, a wynik pozwala uzyskać gotowe wyrażenie, w którym pierwszy ułamek został już pomnożony przez odwrotność ułamka drugiego.
Ta metoda jest implementowana w następujący sposób:
Jeśli na przykład ułamek jest czteropiętrowy, numer znajdujący się na pierwszym piętrze zostaje podniesiony na najwyższe piętro. A figura znajdująca się na drugim piętrze zostaje podniesiona na trzecie piętro. Otrzymane liczby należy połączyć znakami mnożenia (×)

W rezultacie omijając zapis pośredni, otrzymujemy nowe wyrażenie, w którym pierwszy ułamek został już pomnożony przez odwrotność ułamka drugiego. Wygoda i tyle!
Aby uniknąć błędów podczas używania tę metodę możesz kierować się następującą zasadą:
Od pierwszego do czwartego. Od drugiego do trzeciego.
W regule o czym mówimy o podłogach. Postać z pierwszego piętra należy przenieść na czwarte piętro. A figurę z drugiego piętra należy przenieść na trzecie piętro.
Spróbujmy obliczyć ułamek wielopiętrowy, korzystając z powyższej reguły.
Podnosimy więc numer znajdujący się na pierwszym piętrze na czwarte piętro i podnosimy numer znajdujący się na drugim piętrze na trzecie piętro

W rezultacie omijając zapis pośredni, otrzymujemy nowe wyrażenie, w którym pierwszy ułamek został już pomnożony przez odwrotność ułamka drugiego. Następnie możesz wykorzystać swoją istniejącą wiedzę:

Spróbujmy obliczyć ułamek wielopoziomowy, korzystając z nowego schematu.
Są tylko pierwsze, drugie i czwarte piętro. Nie ma trzeciego piętra. Ale nie odchodzimy od podstawowego schematu: podnosimy figurę z pierwszego piętra na czwarte piętro. A ponieważ nie ma trzeciego piętra, numer znajdujący się na drugim piętrze pozostawiamy bez zmian

W rezultacie, pomijając zapis pośredni, otrzymaliśmy nowe wyrażenie, w którym pierwsza liczba -3 została już pomnożona przez odwrotność ułamka drugiej. Następnie możesz wykorzystać swoją istniejącą wiedzę:
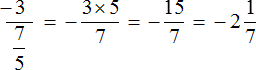
Spróbujmy obliczyć ułamek wielopiętrowy, korzystając z nowego schematu.
Są tylko drugie, trzecie i czwarte piętro. Nie ma pierwszego piętra. Ponieważ nie ma pierwszego piętra, nie ma co wchodzić na czwarte piętro, ale możemy podnieść figurę z drugiego piętra na trzecie:

W rezultacie, omijając zapis pośredni, otrzymaliśmy nowe wyrażenie, w którym pierwszy ułamek został już pomnożony przez odwrotność dzielnika. Następnie możesz wykorzystać swoją istniejącą wiedzę:

Używanie zmiennych
Jeśli wyrażenie jest złożone i wydaje Ci się, że będzie Cię to dezorientowało w procesie rozwiązywania problemu, wówczas część wyrażenia można umieścić w zmiennej i następnie pracować z tą zmienną.
Matematycy często to robią. Trudne zadanie podziel je na łatwiejsze podzadania i rozwiąż je. Następnie rozwiązane podzadania są zbierane w jedną całość. Ten proces twórczy a tego uczy się latami poprzez ciężki trening.
Użycie zmiennych jest uzasadnione w przypadku pracy z ułamkami wielopoziomowymi. Na przykład:
Znajdź wartość wyrażenia
Zatem w liczniku i mianowniku znajduje się wyrażenie ułamkowe, w którym znajdują się wyrażenia ułamkowe. Innymi słowy, znów mamy do czynienia z ułamkiem wielopiętrowym, którego tak bardzo nie lubimy.
Wyrażenie w liczniku można wpisać do zmiennej o dowolnej nazwie, np.:
Ale w matematyce taki przypadek Zwyczajowo nazywa się zmienne wielkimi literami łacińskimi. Nie łammy tej tradycji, a pierwsze wyrażenie oznaczmy dużą Litera łacińska A
![]()
A wyrażenie w mianowniku można oznaczyć wielką literą B
![]()
Teraz nasze oryginalne wyrażenie ma postać . Oznacza to, że dokonaliśmy wymiany wyrażenie numeryczne na literę, po uprzednim wpisaniu licznika i mianownika do zmiennych A i B.
Teraz możemy osobno obliczyć wartości zmiennej A i wartość zmiennej B. Gotowe wartości wstawimy do wyrażenia.
Znajdźmy wartość zmiennej A
Znajdźmy wartość zmiennej B
Podstawmy teraz ich wartości do wyrażenia głównego zamiast zmiennych A i B:

Otrzymaliśmy ułamek wielopiętrowy, w którym możemy zastosować schemat „od pierwszego do czwartego, od drugiego do trzeciego”, czyli podnieść numer znajdujący się na pierwszym piętrze na czwarte piętro i podnieść numer znajdujący się na drugim piętrze na trzecim piętrze. Dalsze obliczenia nie będą trudne:

Zatem wartość wyrażenia wynosi -1.
Oczywiście, że rozważaliśmy najprostszy przykład, ale naszym celem było nauczenie się, jak możemy używać zmiennych, aby sobie ułatwić i zminimalizować błędy.
Należy również zauważyć, że rozwiązanie tego przykładu można zapisać bez użycia zmiennych. To będzie wyglądać

To rozwiązanie jest szybsze i krótsze i w tym przypadku rozsądniej jest zapisać to w ten sposób, ale jeśli wyrażenie okaże się złożone, składające się z kilku parametrów, nawiasów, pierwiastków i potęg, wówczas wskazane jest obliczenie go w kilku etapach, wprowadzając część swoich wyrażeń do zmiennych.
Czy podobała Ci się lekcja?
Dołącz do naszego nowa grupa VKontakte i zacznij otrzymywać powiadomienia o nowych lekcjach





