Ułamki zapisane w postaci 0,8; 0,13; 2,856; 5,2; Wartość 0,04 nazywa się liczbą dziesiętną. W rzeczywistości ułamki dziesiętne są uproszczonym zapisem ułamków zwykłych. Zapis ten jest wygodny w użyciu w przypadku wszystkich ułamków, których mianowniki wynoszą 10, 100, 1000 i tak dalej.

Spójrzmy na przykłady (0,5 jest odczytywane jako zero przecinek pięć);

(0,15 odczytane jako zero przecinek piętnaście);

(5.3 czytaj jako pięć i trzy punkty).

Należy pamiętać, że w zapisie ułamka dziesiętnego część całkowitą liczby od części ułamkowej oddziela przecinek, częścią całkowitą ułamka właściwego jest 0. Zapis części ułamkowej ułamka dziesiętnego zawiera tyle cyfr, ile wynosi w zapisie mianownika odpowiedniego ułamka zwykłego znajdują się zera.

Spójrzmy na przykład, , , .

W niektórych przypadkach może być konieczne potraktowanie liczby naturalnej jako ułamka dziesiętnego, którego część ułamkowa wynosi zero. Zwyczajowo pisze się, że 5 = 5,0; 245 = 245,0 i tak dalej. Należy pamiętać, że w zapisie dziesiętnym liczby naturalnej jednostka najmniej znaczącej cyfry jest 10 razy mniejsza niż jednostka sąsiedniej najbardziej znaczącej cyfry. Zapisywanie ułamków dziesiętnych ma tę samą właściwość. Dlatego bezpośrednio po przecinku znajduje się miejsce dziesiętne, następnie miejsce setne, następnie miejsce tysięczne i tak dalej. Poniżej znajdują się nazwy cyfr liczby 31,85431, dwie pierwsze kolumny to część całkowita, pozostałe kolumny to część ułamkowa.

Ułamek ten odczytuje się jako trzydzieści jeden przecinek osiemdziesiąt pięć tysięcy czterysta trzydzieści sto tysięcznych.

Dodawanie i odejmowanie ułamków dziesiętnych

Pierwszy sposób polega na zamianie ułamków dziesiętnych na zwykłe i wykonaniu dodawania.

Jak widać na przykładzie, metoda ta jest bardzo niewygodna i lepiej zastosować drugą metodę, bardziej poprawną, bez zamiany ułamków dziesiętnych na zwykłe. Aby dodać dwa ułamki dziesiętne należy:

• wyrównać liczbę cyfr po przecinku w wyrazach;
• zapisz wyrazy jeden pod drugim, tak aby każda cyfra drugiego wyrazu znajdowała się pod odpowiednią cyfrą pierwszego wyrazu;
• dodaj powstałe liczby w ten sam sposób, w jaki dodajesz liczby naturalne;
• W otrzymanej sumie umieść przecinek pod przecinkami w terminach.

Spójrzmy na przykłady:

• wyrównać liczbę cyfr po przecinku w odejmowaniu i odejmowaniu;
• wpisz odjemnik pod odjemną końcówką, tak aby każda cyfra odejmowania znajdowała się pod odpowiednią cyfrą odjemnika;
• wykonaj odejmowanie w taki sam sposób, jak odejmuje się liczby naturalne;
• wstaw przecinek w powstałej różnicy pod przecinkami w odejmowaniu i odejmowaniu.

Spójrzmy na przykłady:

Na omówionych powyżej przykładach widać, że dodawanie i odejmowanie ułamków dziesiętnych wykonywaliśmy krok po kroku, czyli w taki sam sposób, w jaki wykonywaliśmy podobne operacje na liczbach naturalnych. Jest to główna zaleta dziesiętnej formy zapisywania ułamków zwykłych.

Mnożenie ułamków dziesiętnych

Aby pomnożyć ułamek dziesiętny przez 10, 100, 1000 itd., należy przesunąć przecinek w tym ułamku w prawo odpowiednio o 1, 2, 3 itd. Dlatego jeśli przecinek zostanie przesunięty w prawo o 1, 2, 3 itd., wówczas ułamek odpowiednio wzrośnie o 10, 100, 1000 i tak dalej. Aby pomnożyć dwa ułamki dziesiętne, należy:

• pomnóż je jako liczby naturalne, ignorując przecinki;
• w otrzymanym iloczynie oddziel przecinkiem po prawej stronie tyle cyfr, ile jest po przecinkach w obu czynnikach razem.

Zdarzają się przypadki, gdy iloczyn zawiera mniej cyfr, niż jest to wymagane do oddzielenia przecinkiem; wymaganą liczbę zer dodaje się z lewej strony przed tym iloczynem, a następnie przecinek przesuwa się w lewo o wymaganą liczbę cyfr.

Spójrzmy na przykłady: 2 * 4 = 8, następnie 0,2 * 0,4 = 0,08; 23 * 35 = 805, następnie 0,023 * 0,35 = 0,00805.

Zdarzają się przypadki, gdy jeden z mnożników jest równy 0,1; 0,01; 0,001 i tak dalej, wygodniej jest zastosować następującą regułę.

• Aby pomnożyć ułamek dziesiętny przez 0,1; 0,01; 0,001 i tak dalej, należy przesunąć przecinek w lewo w tym ułamku dziesiętnym odpowiednio o 1, 2, 3 i tak dalej.

Spójrzmy na przykłady: 2,65 * 0,1 = 0,265; 457,6 * 0,01 = 4,576.

Właściwości mnożenia liczb naturalnych dotyczą także ułamków dziesiętnych.

• ab = ba- przemienność mnożenia;
• (ab) do = a (bc)- asocjacyjna właściwość mnożenia;
• za (b + c) = ab + ac jest właściwością rozdzielczą mnożenia względem dodawania.

Dzielenie dziesiętne

Wiadomo, że jeśli podzielisz liczbę naturalną A do liczby naturalnej B oznacza znalezienie takiej liczby naturalnej C, które po pomnożeniu przez B podaje numer A. Zasada ta pozostaje prawdziwa, jeśli co najmniej jedna z liczb a, b, c jest ułamkiem dziesiętnym.

Spójrzmy na przykład: musisz podzielić 43,52 przez 17 narożnikiem, ignorując przecinek. W takim przypadku przecinek w ilorazu należy postawić bezpośrednio przed pierwszą cyfrą po zastosowaniu przecinka w dzielnej.

Zdarzają się przypadki, gdy dywidenda jest mniejsza niż dzielnik, wówczas część całkowita ilorazu jest równa zero. Spójrzmy na przykład:

Spójrzmy na inny interesujący przykład.

Proces podziału został zatrzymany, ponieważ skończyły się cyfry dywidendy, a na pozostałej części nie ma zera. Wiadomo, że ułamek dziesiętny nie zmieni się, jeśli dodamy do niego dowolną liczbę zer po prawej stronie. Wtedy staje się jasne, że liczby dywidend nie mogą się kończyć.

Aby podzielić ułamek dziesiętny przez 10, 100, 1000 itd., należy przesunąć przecinek w tym ułamku w lewo o 1, 2, 3 itd. Spójrzmy na przykład: 5,14: 10 = 0,514; 2: 100 = 0,02; 37,51: 1000 = 0,03751.

Jeśli dywidenda i dzielnik zostaną zwiększone jednocześnie 10, 100, 1000 itd., wówczas iloraz nie ulegnie zmianie.

Rozważmy przykład: 39,44:1,6 = 24,65, zwiększ dywidendę i dzielnik 10 razy 394,4:16 = 24,65 Warto zauważyć, że dzielenie ułamka dziesiętnego przez liczbę naturalną w drugim przykładzie jest łatwiejsze.

Aby podzielić ułamek dziesiętny przez ułamek dziesiętny, należy:

• przesuń przecinki w dzielnej i dzielniku w prawo o tyle cyfr, ile jest po przecinku w dzielniku;
• podzielić przez liczbę naturalną.

Rozważmy przykład: 23,6: 0,02, zauważ, że dzielnik ma dwa miejsca po przecinku, dlatego mnożymy obie liczby przez 100, otrzymujemy 2360: 2 = 1180, dzielimy wynik przez 100 i otrzymujemy odpowiedź 11,80 lub 23,6: 0, 02 = 11,8.

Porównanie ułamków dziesiętnych

Istnieją dwa sposoby porównywania ułamków dziesiętnych. Metoda pierwsza polega na porównaniu dwóch ułamków dziesiętnych 4,321 i 4,32, wyrównaniu liczby miejsc po przecinku i rozpoczęciu porównywania miejsce po miejscu, dziesiąte z dziesiątymi, setne z setnymi i tak dalej, w końcu otrzymamy 4,321 > 4,320.

Drugi sposób porównywania ułamków dziesiętnych polega na mnożeniu, pomnóż powyższy przykład przez 1000 i porównaj 4321 > 4320. Która metoda jest wygodniejsza, każdy wybiera sam.

Instrukcje

Naucz się konwertować ułamki dziesiętne ułamki do zwykłych. Policz, ile znaków oddziela przecinek. Jedna cyfra na prawo od przecinka oznacza, że ​​mianownik wynosi 10, dwie oznaczają 100, trzy oznaczają 1000 i tak dalej. Na przykład ułamek dziesiętny 6,8 to „sześć i osiem”. Przeliczając, najpierw wpisz liczbę całych jednostek - 6. Wpisz 10 w mianowniku. W liczniku pojawi się liczba 8. Okazuje się, że 6,8 = 6 8/10. Pamiętaj o zasadach skrótów. Jeśli licznik i mianownik są podzielne przez tę samą liczbę, wówczas ułamek można zmniejszyć przez wspólny dzielnik. W w tym przypadku ta liczba to 2,6 8/10 = 6 2/5.

Spróbuj dodać ułamki dziesiętne ułamki. Jeśli zrobisz to w kolumnie, zachowaj ostrożność. Cyfry wszystkich liczb muszą znajdować się ściśle pod sobą - pod przecinkiem. Zasady dodawania są dokładnie takie same, jak w przypadku pracy z plikami . Dodaj kolejny ułamek dziesiętny do tej samej liczby 6,8 - na przykład 7,3. Wpisz trzy poniżej ósemki, przecinek pod przecinkiem i siedem pod szóstką. Zacznij dodawać od ostatniej cyfry. 3+8=11, czyli zapisz 1, zapamiętaj 1. Następnie dodaj 6+7, otrzymasz 13. Dodaj to, co ci zostało w głowie i zapisz wynik - 14,1.

Odejmowanie działa na tej samej zasadzie. Wpisz cyfry pod sobą, a przecinek pod przecinkiem. Zawsze używaj go jako wskazówki, zwłaszcza jeśli liczba cyfr po nim w odejmowaniu jest mniejsza niż w odejmowaniu. Odejmij od podanej liczby, na przykład 2,139. Wpisz dwie cyfry pod szóstką, jedną pod ósmą i pozostałe dwie cyfry pod kolejnymi cyframi, które można oznaczyć jako zera. Okazuje się, że odjemna nie wynosi 6,8, ale 6,800. Wykonując tę ​​akcję otrzymasz w sumie 4.661.

Działania na liczbach ujemnych wykonuje się w taki sam sposób, jak na liczbach. Podczas dodawania minus umieszcza się poza nawiasami, podane liczby umieszcza się w nawiasach, a plus umieszcza się pomiędzy nimi. W końcu się okazuje. Oznacza to, że jeśli dodasz -6,8 i -7,3, otrzymasz ten sam wynik 14,1, ale ze znakiem „-” przed nim. Jeśli odejmowanie jest większe niż odjemnik, wówczas minus jest również usuwany z nawiasu, z więcej mniejsza jest odejmowana. Odejmij -7,3 od 6,8. Przekształć wyrażenie w następujący sposób. 6,8 - 7,3 = -(7,3 - 6,8) = -0,5.

Aby pomnożyć ułamki dziesiętne ułamki, zapomnij na razie o przecinku. Pomnóż je w ten sposób, masz przed sobą liczby całkowite. Następnie policz liczbę cyfr po prawej stronie po przecinku w obu współczynnikach. Oddziel taką samą liczbę znaków w pracy. Mnożąc 6,8 i 7,3, otrzymasz 49,64. Oznacza to, że na prawo od przecinka dziesiętnego będziesz miał 2 znaki, podczas gdy w mnożnej i mnożniku były po jednym.

Podziel podany ułamek przez jakąś liczbę całkowitą. Czynność tę wykonuje się dokładnie w taki sam sposób, jak w przypadku liczb całkowitych. Najważniejsze, aby nie zapomnieć o przecinku i postawić 0 na początku, jeśli liczba całych jednostek nie jest podzielna przez dzielnik. Na przykład spróbuj podzielić tę samą liczbę 6,8 przez 26. Umieść 0 na początku, ponieważ 6 jest mniejsze niż 26. Oddziel je przecinkiem, a po nich pojawią się części dziesiąte i setne. Wynik wyniesie około 0,26. W rzeczywistości w tym przypadku uzyskuje się nieskończoną frakcję nieokresową, którą można zaokrąglić do pożądanego stopnia dokładności.

Dzieląc dwa ułamki dziesiętne, korzystaj z własności, że gdy dzielna i dzielnik zostaną pomnożone przez tę samą liczbę, iloraz się nie zmieni. To znaczy przekształć oba ułamki na liczby całkowite, w zależności od liczby miejsc po przecinku. Jeśli chcesz podzielić 6,8 przez 7,3, po prostu pomnóż obie liczby przez 10. Okazuje się, że musisz podzielić 68 przez 73. Jeśli jedna z liczb ma więcej miejsc po przecinku, przelicz ją najpierw na liczbę całkowitą, a następnie na drugą liczbę. Pomnóż to przez tę samą liczbę. Oznacza to, że dzieląc 6,8 przez 4,136, zwiększ dywidendę i dzielnik nie o 10, ale o 1000 razy. Podziel 6800 przez 1436, aby otrzymać 4,735.

liczba ułamkowa.

Zapis dziesiętny liczby ułamkowej to zbiór dwóch lub więcej cyfr od $0$ do $9$, pomiędzy którymi znajduje się tzw. \textit (przecinek dziesiętny).

Przykład 1

Na przykład 35,02 USD; 100,7 dolarów; 123 $ 456,5 $; 54,89 dolarów.

Najbardziej lewa cyfra w zapisie dziesiętnym liczby nie może wynosić zero, a jedynym wyjątkiem jest sytuacja, gdy przecinek dziesiętny znajduje się bezpośrednio po pierwszej cyfrze $0$.

Przykład 2

Na przykład 0,357 USD; 0,064 $.

Często kropkę dziesiętną zastępuje się kropką dziesiętną. Na przykład 35,02 USD; 100,7 dolarów; 123 $ 456,5 $; 54,89 dolarów.

Definicja dziesiętna

Definicja 1

Dziesiętne -- są to liczby ułamkowe zapisywane w zapisie dziesiętnym.

Na przykład 121,05 USD; 67,9 dolarów; 345,6700 dolarów.

Ułamki dziesiętne służą do bardziej zwięzłego zapisywania ułamków właściwych, których mianownikami są liczby 10 $, 100 $, 1 $\000 $ itd. I liczby mieszane, których mianownikami części ułamkowej są liczby $10$, $100$, $1\000$ itd.

Na przykład, ułamek wspólny$\frac(8)(10)$ można zapisać jako ułamek dziesiętny $0,8$, a liczbę mieszaną $405\frac(8)(100)$ można zapisać jako ułamek dziesiętny $405,08$.

Czytanie ułamków dziesiętnych

Ułamki dziesiętne, które odpowiadają ułamkom zwykłym, czyta się w taki sam sposób, jak ułamki zwykłe, tyle że z przodu dodaje się wyrażenie „zero liczb całkowitych”. Na przykład ułamek zwykły $\frac(25)(100)$ (czytaj „dwadzieścia pięć setnych”) odpowiada ułamkowi dziesiętnemu $0,25$ (czytaj „przecinek zerowy dwadzieścia pięć setnych”).

Ułamki dziesiętne odpowiadające liczbom mieszanym odczytuje się tak samo jak liczby mieszane. Na przykład liczba mieszana 43\frac(15)(1000)$ odpowiada ułamkowi dziesiętnemu 43,015$ (czytaj „czterdzieści trzy i piętnaście tysięcznych”).

Miejsca po przecinku

Zapisując ułamek dziesiętny, znaczenie każdej cyfry zależy od jej położenia. Te. w ułamkach dziesiętnych koncepcja ta ma również zastosowanie kategoria.

Miejsca w ułamkach dziesiętnych przed przecinkiem nazywane są tak samo jak miejsca w liczby naturalne. Miejsca dziesiętne po przecinku podano w tabeli:

Rysunek 1.

Przykład 3

Na przykład w ułamku dziesiętnym 56,328 $, cyfra 5 $ jest na miejscu dziesiątek, 6 $ jest na miejscu jedności, 3 $ jest na miejscu dziesiątym, 2 $ jest na miejscu setnym, 8 $ jest na miejscu tysięcznym miejsce.

Miejsca w ułamkach dziesiętnych są rozróżniane według pierwszeństwa. Czytając ułamek dziesiętny, poruszaj się od lewej do prawej - od senior ranga do mniejszy.

Przykład 4

Na przykład w ułamku dziesiętnym 56,328 $ najbardziej znaczącym (najwyższym) miejscem jest miejsce dziesiątek, a najniższym (najniższym) miejscem tysięcznej.

Ułamek dziesiętny można rozszerzyć na cyfry, podobnie jak rozkład cyfr liczby naturalnej.

Przykład 5

Na przykład podzielmy ułamek dziesiętny 37,851 $ na cyfry:

$37,851=30+7+0,8+0,05+0,001$

Kończenie ułamków dziesiętnych

Definicja 2

Kończenie ułamków dziesiętnych nazywane są ułamkami dziesiętnymi, których zapisy zawierają ostateczny numer znaki (cyfry).

Na przykład 0,138 USD; 5,34 $; 56,123456 $; 350 972,54 dolarów.

Każdy skończony ułamek dziesiętny można zamienić na ułamek zwykły lub liczbę mieszaną.

Przykład 6

Na przykład końcowy ułamek dziesiętny $7,39$ odpowiada liczbie ułamkowej $7\frac(39)(100)$, a końcowy ułamek dziesiętny $0,5$ odpowiada właściwemu ułamkowi wspólnemu $\frac(5)(10)$ (lub dowolny ułamek, który jest jej równy, na przykład $\frac(1)(2)$ lub $\frac(10)(20)$.

Zamiana ułamka zwykłego na dziesiętny

Zamiana ułamków zwykłych o mianownikach $10, 100, \dots$ na ułamki dziesiętne

Przed zamianą niektórych ułamków właściwych na dziesiętne należy je najpierw „przygotować”. Wynikiem takiego przygotowania powinna być taka sama liczba cyfr w liczniku i taka sama liczba zer w mianowniku.

Istota „ wstępne przygotowanie» zamiana ułamków zwykłych na dziesiętne - dodanie takiej liczby zer z lewej strony licznika, aby suma cyfr była równa liczbie zer w mianowniku.

Przykład 7

Na przykład przygotujmy ułamek $\frac(43)(1000)$ do konwersji na ułamek dziesiętny i otrzymamy $\frac(043)(1000)$. A zwykły ułamek $\frac(83)(100)$ nie wymaga żadnego przygotowania.

Sformułujmy reguła zamiany właściwego ułamka zwykłego o mianowniku 10$, 100$ lub 1\000$, $\dots$ na ułamek dziesiętny:

napisz $0$;

po nim wstaw przecinek dziesiętny;

zapisz liczbę z licznika (wraz z dodanymi zerami po przygotowaniu, jeśli to konieczne).

Przykład 8

Zamień ułamek właściwy $\frac(23)(100)$ na ułamek dziesiętny.

Rozwiązanie.

W mianowniku znajduje się liczba 100 $, która zawiera 2 $ i dwa zera. Licznik zawiera liczbę $23$, którą zapisuje się za pomocą $2$.cyfr. Oznacza to, że nie ma potrzeby przygotowywania tego ułamka do zamiany na ułamek dziesiętny.

Zapiszmy $0$, postawmy przecinek dziesiętny i zapiszmy z licznika liczbę $23$. Otrzymujemy ułamek dziesiętny 0,23 $.

Odpowiedź: $0,23$.

Przykład 9

Zapisz odpowiedni ułamek $\frac(351)(100000)$ jako ułamek dziesiętny.

Rozwiązanie.

Licznik tego ułamka zawiera cyfry 3$, a liczba zer w mianowniku wynosi 5$, więc ten ułamek zwykły trzeba przygotować do zamiany na ułamek dziesiętny. Aby to zrobić, musisz dodać zera $5-3=2$ po lewej stronie licznika: $\frac(00351)(100000)$.

Teraz możemy utworzyć żądany ułamek dziesiętny. Aby to zrobić, wpisz $0$, następnie dodaj przecinek i zapisz liczbę z licznika. Otrzymujemy ułamek dziesiętny 0,00351 $.

Odpowiedź: $0,00351$.

Sformułujmy reguła zamiany ułamków niewłaściwych o mianownikach $10$, $100$, $\dots$ na ułamki dziesiętne:

zapisz liczbę z licznika;

Użyj kropki dziesiętnej, aby oddzielić tyle cyfr po prawej stronie, ile jest zer w mianowniku pierwotnego ułamka.

Przykład 10

Zamień ułamek niewłaściwy $\frac(12756)(100)$ na ułamek dziesiętny.

Rozwiązanie.

Zapiszmy liczbę z licznika 12756 $, a następnie oddzielmy cyfry 2 $ po prawej stronie przecinkiem, ponieważ mianownik pierwotnego ułamka $2$ wynosi zero. Otrzymujemy ułamek dziesiętny 127,56 $.

W tym samouczku przyjrzymy się każdej z tych operacji osobno.

Treść lekcji

Dodawanie ułamków dziesiętnych

Jak wiemy, ułamek dziesiętny składa się z liczby całkowitej i części ułamkowej. Podczas dodawania ułamków dziesiętnych części całkowite i ułamkowe dodawane są osobno.

Na przykład dodajmy ułamki dziesiętne 3,2 i 5,3. Wygodniej jest dodawać ułamki dziesiętne w kolumnie.

Zapiszmy najpierw te dwa ułamki w kolumnie, tak aby części całkowite znajdowały się pod liczbami całkowitymi, a ułamki pod ułamkami. W szkole ten wymóg nazywa się „przecinek pod przecinkiem”.

Zapiszmy ułamki w kolumnie tak, aby przecinek znalazł się pod przecinkiem:

Zaczynamy dodawać części ułamkowe: 2 + 3 = 5. Piątkę wpisujemy w części ułamkowej naszej odpowiedzi:

Teraz dodajemy całe części: 3 + 5 = 8. W całej części naszej odpowiedzi wpisujemy ósemkę:

Teraz oddzielamy całą część od części ułamkowej przecinkiem. Aby to zrobić, ponownie postępujemy zgodnie z regułą „przecinek pod przecinkiem”:

Otrzymaliśmy odpowiedź 8,5. Zatem wyrażenie 3,2 + 5,3 równa się 8,5

Tak naprawdę nie wszystko jest tak proste, jak się wydaje na pierwszy rzut oka. Istnieją również pułapki, o których teraz porozmawiamy.

Miejsca po przecinku

Ułamki dziesiętne, podobnie jak zwykłe liczby, mają swoje własne cyfry. Są to miejsca dziesiątych, setnych i tysięcznych. W tym przypadku cyfry zaczynają się po przecinku.

Pierwsza cyfra po przecinku odpowiada za miejsce dziesiętne, druga cyfra po przecinku za miejsce setne, zaś trzecia cyfra po przecinku za miejsce tysięczne.

Miejsca dziesiętne zawierają przydatne informacje. W szczególności mówią ci, ile części dziesiętnych, setnych i tysięcznych mieści się w ułamku dziesiętnym.

Rozważmy na przykład ułamek dziesiętny 0,345

Pozycja, w której znajduje się trójka, nazywa się dziesiąte miejsce

Pozycja, w której znajduje się czwórka, nazywa się setne miejsce

Pozycja, w której znajduje się piątka, nazywa się tysięczne miejsce

Spójrzmy ten rysunek. Widzimy, że na dziesiątym miejscu jest trójka. Oznacza to, że w ułamku dziesiętnym 0,345 znajdują się trzy dziesiąte.

Jeśli dodamy ułamki zwykłe, otrzymamy pierwotny ułamek dziesiętny 0,345

Widać, że na początku otrzymaliśmy odpowiedź, ale przeliczyliśmy ją na ułamek dziesiętny i otrzymaliśmy 0,345.

Dodając ułamki dziesiętne, przestrzegaj tych samych zasad i reguł, co przy dodawaniu zwykłych liczb. Dodawanie ułamków dziesiętnych odbywa się za pomocą cyfr: dziesiąte dodaje się do dziesiątych, setne do setnych, tysięczne do tysięcznych.

Dlatego dodając ułamki dziesiętne, musisz przestrzegać reguły „przecinek pod przecinkiem”. Przecinek pod przecinkiem określa kolejność dodawania dziesiątych do dziesiątych, setnych do setnych, tysięcznych do tysięcznych.

Przykład 1. Znajdź wartość wyrażenia 1,5 + 3,4

Najpierw dodajemy części ułamkowe 5 + 4 = 9. W części ułamkowej naszej odpowiedzi piszemy dziewięć:

Teraz dodajemy części całkowite 1 + 3 = 4. Czwórkę wpisujemy w części całkowitej naszej odpowiedzi:

Teraz oddzielamy całą część od części ułamkowej przecinkiem. Aby to zrobić, ponownie stosujemy zasadę „przecinek pod przecinkiem”:

Otrzymaliśmy odpowiedź 4,9. Oznacza to, że wartość wyrażenia 1,5 + 3,4 wynosi 4,9

Przykład 2. Znajdź wartość wyrażenia: 3,51 + 1,22

To wyrażenie zapisujemy w kolumnie, przestrzegając zasady „przecinek pod przecinkiem”.

Najpierw dodajemy część ułamkową, czyli setne części 1+2=3. W setnej części naszej odpowiedzi piszemy trójkę:

Teraz dodaj części dziesiąte 5+2=7. W dziesiątej części naszej odpowiedzi wpisujemy siódemkę:

Teraz dodajemy całe części 3+1=4. Czwórkę piszemy w całej części naszej odpowiedzi:

Część całkowitą od części ułamkowej oddzielamy przecinkiem, zachowując zasadę „przecinek pod przecinkiem”:

Odpowiedź jaką otrzymaliśmy to 4,73. Oznacza to, że wartość wyrażenia 3,51 + 1,22 wynosi 4,73

3,51 + 1,22 = 4,73

Podobnie jak w przypadku zwykłych liczb, podczas dodawania ułamków dziesiętnych, . W takim przypadku w odpowiedzi zapisuje się jedną cyfrę, a resztę przenosi się na następną cyfrę.

Przykład 3. Znajdź wartość wyrażenia 2,65 + 3,27

Zapisujemy to wyrażenie w kolumnie:

Dodaj części setne 5+7=12. Liczba 12 nie zmieści się w setnej części naszej odpowiedzi. Dlatego w części setnej zapisujemy liczbę 2 i przenosimy jednostkę do kolejnej cyfry:

Teraz dodajemy dziesiąte części 6 + 2 = 8 plus jednostkę otrzymaną z poprzedniej operacji i otrzymujemy 9. Liczbę 9 wpisujemy w dziesiątej części naszej odpowiedzi:

Teraz dodajemy całe części 2+3=5. W części całkowitej naszej odpowiedzi wpisujemy cyfrę 5:

Odpowiedź jaką otrzymaliśmy to 5,92. Oznacza to, że wartość wyrażenia 2,65 + 3,27 wynosi 5,92

2,65 + 3,27 = 5,92

Przykład 4. Znajdź wartość wyrażenia 9,5 + 2,8

Zapisujemy to wyrażenie w kolumnie

Dodajemy części ułamkowe 5 + 8 = 13. Liczba 13 nie zmieści się w części ułamkowej naszej odpowiedzi, więc najpierw zapisujemy liczbę 3 i przenosimy jednostkę do następnej cyfry, a raczej przenosimy ją do część całkowita:

Teraz dodajemy części całkowite 9+2=11 plus jednostkę otrzymaną z poprzedniej operacji i otrzymujemy 12. Liczbę 12 wpisujemy w części całkowitej naszej odpowiedzi:

Oddziel część całą od części ułamkowej przecinkiem:

Otrzymaliśmy odpowiedź 12.3. Oznacza to, że wartość wyrażenia 9,5 + 2,8 wynosi 12,3

9,5 + 2,8 = 12,3

Podczas dodawania ułamków dziesiętnych liczba cyfr po przecinku w obu ułamkach musi być taka sama. Jeśli nie ma wystarczającej liczby liczb, wówczas te miejsca w części ułamkowej są wypełniane zerami.

Przykład 5. Znajdź wartość wyrażenia: 12,725 + 1,7

Zanim zapiszemy to wyrażenie w kolumnie, sprawmy, aby liczba cyfr po przecinku w obu ułamkach była taka sama. Ułamek dziesiętny 12,725 ma trzy cyfry po przecinku, ale ułamek 1,7 ma tylko jedną. Oznacza to, że we frakcji 1,7 należy dodać na końcu dwa zera. Następnie otrzymujemy ułamek 1,700. Teraz możesz zapisać to wyrażenie w kolumnie i rozpocząć obliczenia:

Dodaj części tysięczne 5+0=5. W tysięcznej części naszej odpowiedzi wpisujemy cyfrę 5:

Dodaj części setne 2+0=2. W setnej części naszej odpowiedzi zapisujemy cyfrę 2:

Dodaj części dziesiąte 7+7=14. Liczba 14 nie zmieści się w jednej dziesiątej naszej odpowiedzi. Dlatego najpierw zapisujemy liczbę 4 i przenosimy jednostkę do następnej cyfry:

Teraz dodajemy części całkowite 12+1=13 plus jednostkę otrzymaną z poprzedniej operacji i otrzymujemy 14. Liczbę 14 wpisujemy w części całkowitej naszej odpowiedzi:

Oddziel część całą od części ułamkowej przecinkiem:

Otrzymaliśmy odpowiedź 14 425. Oznacza to, że wartość wyrażenia 12,725+1,700 wynosi 14,425

12,725+ 1,700 = 14,425

Odejmowanie ułamków dziesiętnych

Odejmując ułamki dziesiętne należy zachować takie same zasady jak przy dodawaniu: „przecinek pod przecinkiem” i „równą liczbę cyfr po przecinku”.

Przykład 1. Znajdź wartość wyrażenia 2,5 - 2,2

To wyrażenie zapisujemy w kolumnie, przestrzegając zasady „przecinek pod przecinkiem”:

Obliczamy część ułamkową 5−2=3. W dziesiątej części naszej odpowiedzi wpisujemy cyfrę 3:

Obliczamy część całkowitą 2−2=0. W części całkowitej naszej odpowiedzi zapisujemy zero:

Oddziel część całą od części ułamkowej przecinkiem:

Otrzymaliśmy odpowiedź 0,3. Oznacza to, że wartość wyrażenia 2,5 − 2,2 jest równa 0,3

2,5 − 2,2 = 0,3

Przykład 2. Znajdź wartość wyrażenia 7,353 - 3,1

To wyrażenie ma inną liczbę miejsc po przecinku. Ułamek 7,353 ma trzy cyfry po przecinku, ale ułamek 3,1 ma tylko jedną. Oznacza to, że we ułamku 3.1 należy dodać na końcu dwa zera, aby liczba cyfr w obu ułamkach była taka sama. Wtedy otrzymamy 3100.

Teraz możesz zapisać to wyrażenie w kolumnie i obliczyć:

Otrzymaliśmy odpowiedź 4253. Oznacza to, że wartość wyrażenia 7,353 - 3,1 jest równa 4,253

7,353 — 3,1 = 4,253

Podobnie jak w przypadku zwykłych liczb, czasami będziesz musiał pożyczyć jedną z sąsiedniej cyfry, jeśli odejmowanie stanie się niemożliwe.

Przykład 3. Znajdź wartość wyrażenia 3,46 - 2,39

Odejmij setne części 6-9. Nie możesz odjąć liczby 9 od liczby 6. Dlatego musisz pożyczyć cyfrę od sąsiedniej cyfry. Pożyczając jedynkę z sąsiedniej cyfry, liczba 6 zamienia się w liczbę 16. Teraz możesz obliczyć setne części 16−9=7. W setnej części naszej odpowiedzi wpisujemy siódemkę:

Teraz odejmujemy dziesiątki. Ponieważ na dziesiątym miejscu zajęliśmy jedną jednostkę, znajdująca się tam liczba zmniejszyła się o jedną jednostkę. Innymi słowy, na miejscu dziesiątym nie znajduje się teraz liczba 4, ale liczba 3. Obliczmy dziesiąte części 3−3=0. W dziesiątej części naszej odpowiedzi zapisujemy zero:

Teraz odejmujemy całe części 3−2=1. W części całkowitej naszej odpowiedzi zapisujemy jedynkę:

Oddziel część całą od części ułamkowej przecinkiem:

Otrzymaliśmy odpowiedź 1.07. Oznacza to, że wartość wyrażenia 3,46−2,39 jest równa 1,07

3,46−2,39=1,07

Przykład 4. Znajdź wartość wyrażenia 3−1,2

W tym przykładzie odejmuje się ułamek dziesiętny od liczby całkowitej. Zapiszmy to wyrażenie w kolumnie tak, aby cała część ułamka dziesiętnego 1,23 znalazła się pod liczbą 3

Teraz sprawmy, aby liczba cyfr po przecinku była taka sama. Aby to zrobić, po liczbie 3 stawiamy przecinek i dodajemy jedno zero:

Teraz odejmujemy dziesiąte: 0-2. Nie możesz odjąć liczby 2 od zera, dlatego musisz pożyczyć jedynkę od sąsiedniej cyfry. Pożyczając jedynkę od sąsiedniej cyfry, 0 zamienia się w liczbę 10. Teraz możesz obliczyć dziesiąte części 10−2=8. W dziesiątej części naszej odpowiedzi wpisujemy ósemkę:

Teraz odejmujemy całe części. Poprzednio cyfra 3 znajdowała się w całości, ale my wzięliśmy z niej jedną jednostkę. W rezultacie zamieniło się w liczbę 2. Dlatego od 2 odejmujemy 1. 2−1=1. W części całkowitej naszej odpowiedzi zapisujemy jedynkę:

Oddziel część całą od części ułamkowej przecinkiem:

Odpowiedź jaką otrzymaliśmy to 1,8. Oznacza to, że wartość wyrażenia 3−1,2 wynosi 1,8

Mnożenie ułamków dziesiętnych

Mnożenie ułamków dziesiętnych jest proste, a nawet przyjemne. Aby pomnożyć ułamki dziesiętne, mnożysz je jak zwykłe liczby, ignorując przecinki.

Po otrzymaniu odpowiedzi należy oddzielić całą część od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w obu ułamkach, a następnie policzyć tę samą liczbę cyfr od prawej strony w odpowiedzi i postawić przecinek.

Przykład 1. Znajdź wartość wyrażenia 2,5 × 1,5

Pomnóżmy te ułamki dziesiętne jak zwykłe liczby, ignorując przecinki. Aby zignorować przecinki, możesz tymczasowo wyobrazić sobie, że są one całkowicie nieobecne:

Mamy 375. W tej liczbie należy oddzielić część całkowitą od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamkach 2,5 i 1,5. Pierwszy ułamek ma jedną cyfrę po przecinku, drugi ułamek również ma jedną cyfrę. W sumie dwie liczby.

Wracamy do liczby 375 i zaczynamy poruszać się od prawej do lewej. Musimy policzyć dwie cyfry po prawej stronie i postawić przecinek:

Otrzymaliśmy odpowiedź 3,75. Zatem wartość wyrażenia 2,5 × 1,5 wynosi 3,75

2,5 × 1,5 = 3,75

Przykład 2. Znajdź wartość wyrażenia 12,85 × 2,7

Pomnóżmy te ułamki dziesiętne, ignorując przecinki:

Otrzymaliśmy 34695. W tej liczbie należy oddzielić część całkowitą od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamkach 12,85 i 2,7. Ułamek 12,85 ma dwie cyfry po przecinku, a ułamek 2,7 ma jedną cyfrę – w sumie trzy cyfry.

Wracamy do numeru 34695 i zaczynamy poruszać się od prawej do lewej. Musimy policzyć trzy cyfry od prawej strony i postawić przecinek:

Otrzymaliśmy odpowiedź 34 695. Zatem wartość wyrażenia 12,85 × 2,7 wynosi 34,695

12,85 × 2,7 = 34,695

Mnożenie ułamka dziesiętnego przez liczbę zwykłą

Czasami pojawiają się sytuacje, gdy trzeba pomnożyć ułamek dziesiętny przez liczbę zwykłą.

Aby pomnożyć ułamek dziesiętny i liczbę, mnożysz je bez zwracania uwagi na przecinek w miejscu dziesiętnym. Po otrzymaniu odpowiedzi należy oddzielić całą część od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamku dziesiętnym, a następnie policzyć tę samą liczbę cyfr od prawej strony w odpowiedzi i postawić przecinek.

Na przykład pomnóż 2,54 przez 2

Pomnóż ułamek dziesiętny 2,54 przez zwykłą liczbę 2, ignorując przecinek:

Otrzymaliśmy liczbę 508. W tej liczbie należy oddzielić część całkowitą od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamku 2,54. Ułamek 2,54 ma dwie cyfry po przecinku.

Wracamy do numeru 508 i zaczynamy poruszać się od prawej do lewej. Musimy policzyć dwie cyfry po prawej stronie i postawić przecinek:

Otrzymaliśmy odpowiedź 5.08. Zatem wartość wyrażenia 2,54 × 2 wynosi 5,08

2,54 × 2 = 5,08

Mnożenie ułamków dziesiętnych przez 10, 100, 1000

Mnożenie ułamków dziesiętnych przez 10, 100 lub 1000 odbywa się w taki sam sposób, jak mnożenie ułamków dziesiętnych przez liczby zwykłe. Należy wykonać mnożenie, nie zwracając uwagi na przecinek w ułamku dziesiętnym, a następnie oddzielić całą część od części ułamkowej w odpowiedzi, licząc od prawej strony tyle cyfr, ile było cyfr po przecinku.

Na przykład pomnóż 2,88 przez 10

Pomnóż ułamek dziesiętny 2,88 przez 10, ignorując przecinek w ułamku dziesiętnym:

Mamy 2880. W tej liczbie należy oddzielić część całkowitą od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamku 2,88. Widzimy, że ułamek 2,88 ma dwie cyfry po przecinku.

Wracamy do liczby 2880 i zaczynamy poruszać się od prawej do lewej. Musimy policzyć dwie cyfry po prawej stronie i postawić przecinek:

Otrzymaliśmy odpowiedź 28,80. Odrzućmy ostatnie zero i otrzymajmy 28,8. Oznacza to, że wartość wyrażenia 2,88×10 wynosi 28,8

2,88 × 10 = 28,8

Istnieje drugi sposób mnożenia ułamków dziesiętnych przez 10, 100, 1000. Ta metoda jest znacznie prostsza i wygodniejsza. Polega na przesunięciu przecinka w prawo o tyle cyfr, ile jest zer w współczynniku.

Na przykład rozwiążmy w ten sposób poprzedni przykład 2,88×10. Nie wykonując żadnych obliczeń, od razu patrzymy na współczynnik 10. Interesuje nas, ile jest w nim zer. Widzimy, że jest w nim jedno zero. Teraz w ułamku 2,88 przesuwamy przecinek w prawo o jedną cyfrę, otrzymujemy 28,8.

2,88 × 10 = 28,8

Spróbujmy pomnożyć 2,88 przez 100. Od razu patrzymy na współczynnik 100. Interesuje nas, ile jest w nim zer. Widzimy, że są w nim dwa zera. Teraz w ułamku 2,88 przesuwamy przecinek w prawo o dwie cyfry, otrzymujemy 288

2,88 × 100 = 288

Spróbujmy pomnożyć 2,88 przez 1000. Od razu patrzymy na współczynnik 1000. Interesuje nas, ile jest w nim zer. Widzimy, że są w nim trzy zera. Teraz we ułamku 2,88 przesuwamy przecinek w prawo o trzy cyfry. Nie ma tam trzeciej cyfry, więc dodajemy kolejne zero. W rezultacie otrzymujemy 2880.

2,88 × 1000 = 2880

Mnożenie ułamków dziesiętnych przez 0,1 0,01 i 0,001

Mnożenie ułamków dziesiętnych przez 0,1, 0,01 i 0,001 działa w taki sam sposób, jak mnożenie ułamka dziesiętnego przez ułamek dziesiętny. Należy pomnożyć ułamki zwykłe jak liczby, a w odpowiedzi postawić przecinek, licząc po prawej stronie tyle cyfr, ile jest cyfr po przecinku w obu ułamkach.

Na przykład pomnóż 3,25 przez 0,1

Mnożymy te ułamki jak zwykłe liczby, ignorując przecinki:

Mamy 325. W tej liczbie należy oddzielić część całkowitą od części ułamkowej przecinkiem. Aby to zrobić, musisz policzyć liczbę cyfr po przecinku w ułamkach 3,25 i 0,1. Ułamek 3,25 ma dwie cyfry po przecinku, a ułamek 0,1 ma jedną cyfrę. Razem trzy liczby.

Wracamy do liczby 325 i zaczynamy poruszać się od prawej do lewej. Musimy policzyć trzy cyfry od prawej strony i postawić przecinek. Po odliczeniu trzech cyfr stwierdzamy, że cyfry się wyczerpały. W takim przypadku musisz dodać jedno zero i dodać przecinek:

Otrzymaliśmy odpowiedź 0,325. Oznacza to, że wartość wyrażenia 3,25 × 0,1 wynosi 0,325

3,25 × 0,1 = 0,325

Istnieje drugi sposób mnożenia ułamków dziesiętnych przez 0,1, 0,01 i 0,001. Ta metoda jest znacznie prostsza i wygodniejsza. Polega na przesunięciu przecinka w lewo o tyle cyfr, ile jest zer w współczynniku.

Na przykład rozwiążmy w ten sposób poprzedni przykład 3,25 × 0,1. Nie podając żadnych obliczeń, od razu patrzymy na mnożnik 0,1. Interesuje nas, ile jest w nim zer. Widzimy, że jest w nim jedno zero. Teraz w ułamku 3,25 przesuwamy przecinek w lewo o jedną cyfrę. Przesuwając przecinek o jedną cyfrę w lewo, widzimy, że przed trójką nie ma już więcej cyfr. W takim przypadku dodaj jedno zero i wstaw przecinek. Wynik to 0,325

3,25 × 0,1 = 0,325

Spróbujmy pomnożyć 3,25 przez 0,01. Natychmiast patrzymy na mnożnik 0,01. Interesuje nas, ile jest w nim zer. Widzimy, że są w nim dwa zera. Teraz we ułamku 3,25 przesuwamy przecinek w lewo o dwie cyfry, otrzymujemy 0,0325

3,25 × 0,01 = 0,0325

Spróbujmy pomnożyć 3,25 przez 0,001. Natychmiast patrzymy na mnożnik 0,001. Interesuje nas, ile jest w nim zer. Widzimy, że są w nim trzy zera. Teraz w ułamku 3,25 przesuwamy przecinek w lewo o trzy cyfry, otrzymujemy 0,00325

3,25 × 0,001 = 0,00325

Nie myl mnożenia ułamków dziesiętnych przez 0,1, 0,001 i 0,001 z mnożeniem przez 10, 100, 1000. Typowy błąd większości ludzi.

Przy mnożeniu przez 10, 100, 1000 przecinek dziesiętny przesuwa się w prawo o tę samą liczbę cyfr, ile jest zer w mnożniku.

A przy mnożeniu przez 0,1, 0,01 i 0,001 przecinek dziesiętny przesuwa się w lewo o tę samą liczbę cyfr, ile jest zer w mnożniku.

Jeśli na początku trudno jest to zapamiętać, możesz zastosować pierwszą metodę, w której mnożenie wykonuje się jak w przypadku zwykłych liczb. W odpowiedzi będziesz musiał oddzielić część całą od części ułamkowej, licząc po prawej stronie tyle cyfr, ile jest cyfr po przecinku w obu ułamkach.

Dzielenie mniejszej liczby przez większą liczbę. Poziom zaawansowany.

Na jednej z poprzednich lekcji powiedzieliśmy, że dzieląc mniejszą liczbę przez większą liczbę, otrzymujemy ułamek, którego licznik jest dzielną, a mianownik jest dzielnikiem.

Na przykład, aby podzielić jedno jabłko między dwa, musisz wpisać 1 (jedno jabłko) w liczniku i wpisać 2 (dwóch przyjaciół) w mianowniku. W rezultacie otrzymujemy ułamek . Oznacza to, że każdy przyjaciel otrzyma jabłko. Innymi słowy, pół jabłka. Ułamek jest odpowiedzią na problem „Jak podzielić jedno jabłko na dwa”

Okazuje się, że możesz rozwiązać ten problem dalej, dzieląc 1 przez 2. Przecież linia ułamkowa w dowolnym ułamku oznacza dzielenie, dlatego ten podział jest dozwolony w ułamku. Ale jak? Przyzwyczailiśmy się, że dywidenda jest zawsze większa niż dzielnik. Ale wręcz przeciwnie, dywidenda jest mniejsza niż dzielnik.

Wszystko stanie się jasne, jeśli przypomnimy sobie, że ułamek oznacza miażdżenie, dzielenie, dzielenie. Oznacza to, że urządzenie można podzielić na dowolną liczbę części, a nie tylko na dwie części.

Dzieląc mniejszą liczbę przez większą liczbę, otrzymujesz ułamek dziesiętny, którego częścią całkowitą jest 0 (zero). Część ułamkowa może być dowolna.

Podzielmy więc 1 przez 2. Rozwiążmy ten przykład za pomocą rogu:

Jednego nie da się całkowicie podzielić na dwa. Jeśli zadasz pytanie „Ile dwójek jest w jednym” , wówczas odpowiedzią będzie 0. Dlatego w ilorazie piszemy 0 i stawiamy przecinek:

Teraz jak zwykle mnożymy iloraz przez dzielnik, aby otrzymać resztę:

Nadszedł moment, w którym jednostkę można podzielić na dwie części. Aby to zrobić, dodaj kolejne zero po prawej stronie wynikowego:

Otrzymaliśmy 10. Podzielmy 10 przez 2 i otrzymamy 5. Piątkę zapisujemy w części ułamkowej naszej odpowiedzi:

Teraz usuwamy ostatnią resztę, aby zakończyć obliczenia. Pomnóż 5 przez 2, aby otrzymać 10

Otrzymaliśmy odpowiedź 0,5. Zatem ułamek wynosi 0,5

Połówkę jabłka można również zapisać przy użyciu ułamka dziesiętnego 0,5. Jeśli dodamy te dwie połówki (0,5 i 0,5), ponownie otrzymamy oryginalne całe jabłko:

Ten punkt można również zrozumieć, jeśli wyobrazisz sobie, jak 1 cm jest podzielony na dwie części. Jeśli podzielisz 1 centymetr na 2 części, otrzymasz 0,5 cm

Przykład 2. Znajdź wartość wyrażenia 4:5

Ile piątek jest w czwórce? Zupełnie nie. W iloraz wpisujemy 0 i stawiamy przecinek:

Mnożymy 0 przez 5, otrzymujemy 0. Pod czwórką piszemy zero. Natychmiast odejmij to zero od dywidendy:

Teraz zacznijmy dzielić (dzielić) cztery na 5 części. Aby to zrobić, dodaj zero po prawej stronie 4 i podziel 40 przez 5, otrzymamy 8. W iloraz zapisujemy osiem.

Uzupełniamy przykład, mnożąc 8 przez 5, aby otrzymać 40:

Otrzymaliśmy odpowiedź 0,8. Oznacza to, że wartość wyrażenia 4:5 wynosi 0,8

Przykład 3. Znajdź wartość wyrażenia 5: 125

Ile liczb jest 125 w pięciu? Zupełnie nie. W iloraz wpisujemy 0 i stawiamy przecinek:

Mnożymy 0 przez 5, otrzymujemy 0. Pod piątką piszemy 0. Natychmiast odejmij 0 od pięciu

Teraz zacznijmy dzielić (dzielić) tę piątkę na 125 części. Aby to zrobić, napiszemy zero po prawej stronie tej piątki:

Podziel 50 przez 125. Ile liczb wynosi 125 w liczbie 50? Zupełnie nie. Zatem w ilorazie ponownie piszemy 0

Pomnóż 0 przez 125, otrzymamy 0. Zapisz to zero pod 50. Natychmiast odejmij 0 od 50

Teraz podziel liczbę 50 na 125 części. Aby to zrobić, zapisujemy kolejne zero po prawej stronie 50:

Podziel 500 przez 125. Ile liczb 125 znajduje się w liczbie 500. W liczbie 500 znajdują się cztery liczby 125. Wpisz cztery w iloraz:

Uzupełniamy przykład, mnożąc 4 przez 125, aby otrzymać 500

Otrzymaliśmy odpowiedź 0,04. Oznacza to, że wartość wyrażenia 5:125 wynosi 0,04

Dzielenie liczb bez reszty

Zatem postawmy przecinek po jednostce ilorazu, sygnalizując tym samym, że dzielenie części całkowitych zostało zakończone i przechodzimy do części ułamkowej:

Dodajmy zero do reszty 4

Teraz podziel 40 przez 5, otrzymamy 8. W iloraz zapisujemy osiem:

40−40=0. Zostało nam 0. Oznacza to, że podział jest całkowicie zakończony. Dzielenie 9 przez 5 daje ułamek dziesiętny 1,8:

9: 5 = 1,8

Przykład 2. Podziel 84 przez 5 bez reszty

Najpierw podziel 84 przez 5 jak zwykle z resztą:

Prywatnie zostało nas 16, zostały jeszcze 4. Teraz podzielmy tę resztę przez 5. W iloraz wstaw przecinek i dodaj 0 do reszty 4

Teraz dzielimy 40 przez 5, otrzymujemy 8. Ósemkę zapisujemy w iloraz po przecinku:

i uzupełnij przykład, sprawdzając, czy jest jeszcze reszta:

Dzielenie ułamka dziesiętnego przez liczbę zwykłą

Jak wiemy, ułamek dziesiętny składa się z liczby całkowitej i części ułamkowej. Dzieląc ułamek dziesiętny przez liczbę zwykłą, najpierw musisz:

• podziel całą część ułamka dziesiętnego przez tę liczbę;
• po podzieleniu całej części należy natychmiast wstawić przecinek w iloraz i kontynuować obliczenia jak przy normalnym dzieleniu.

Na przykład podziel 4,8 przez 2

Zapiszmy ten przykład w rogu:

Teraz podzielmy całą część przez 2. Cztery podzielone przez dwa równa się dwa. W iloraz piszemy dwa i natychmiast stawiamy przecinek:

Teraz mnożymy iloraz przez dzielnik i sprawdzamy, czy z dzielenia zostanie reszta:

4-4=0. Reszta równy zeru. Nie zapisujemy jeszcze zera, ponieważ rozwiązanie nie jest ukończone. Następnie kontynuujemy obliczenia jak przy zwykłym dzieleniu. Odejmij 8 i podziel przez 2

8: 2 = 4. Czwórkę zapisujemy w ilorazu i natychmiast mnożymy przez dzielnik:

Otrzymaliśmy odpowiedź 2,4. Wartość wyrażenia 4,8:2 wynosi 2,4

Przykład 2. Znajdź wartość wyrażenia 8,43: 3

Podziel 8 przez 3, otrzymamy 2. Natychmiast postaw przecinek po 2:

Teraz mnożymy iloraz przez dzielnik 2 × 3 = 6. Sześć zapisujemy pod ósmą i znajdujemy resztę:

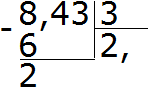
Podziel 24 przez 3, otrzymamy 8. W iloraz zapisujemy osiem. Natychmiast pomnóż go przez dzielnik, aby znaleźć resztę dzielenia:

24-24=0. Reszta wynosi zero. Nie zapisujemy jeszcze zera. Odejmujemy ostatnie trzy z dywidendy i dzielimy przez 3, otrzymujemy 1. Natychmiast pomnóż 1 przez 3, aby zakończyć ten przykład:

Odpowiedź jaką otrzymaliśmy to 2,81. Oznacza to, że wartość wyrażenia 8,43:3 wynosi 2,81

Dzielenie ułamka dziesiętnego przez ułamek dziesiętny

Aby podzielić ułamek dziesiętny przez ułamek dziesiętny, należy przesunąć przecinek dziesiętny w dywidendzie i dzielniku w prawo o tę samą liczbę cyfr, ile jest po przecinku w dzielniku, a następnie podzielić przez zwykłą liczbę.

Na przykład podziel 5,95 przez 1,7

Zapiszmy to wyrażenie z rogiem

Teraz w dzielnej i dzielniku przesuwamy przecinek w prawo o tę samą liczbę cyfr, ile jest po przecinku w dzielniku. Dzielnik ma jedną cyfrę po przecinku. Oznacza to, że w dzielnej i dzielniku musimy przesunąć przecinek w prawo o jedną cyfrę. Przenosimy:

Po przesunięciu przecinka w prawo o jedną cyfrę, ułamek dziesiętny 5,95 stał się ułamkiem 59,5. A ułamek dziesiętny 1,7 po przesunięciu przecinka w prawo o jedną cyfrę zamienił się w zwykłą liczbę 17. I już wiemy, jak podzielić ułamek dziesiętny przez liczbę zwykłą. Dalsze obliczenia nie są trudne:

Przecinek przesunięto w prawo, aby ułatwić dzielenie. Jest to dozwolone, ponieważ przy mnożeniu lub dzieleniu dywidendy i dzielnika przez tę samą liczbę iloraz się nie zmienia. Co to znaczy?

To jest jeden z ciekawe funkcje dział. Nazywa się to właściwością ilorazu. Rozważ wyrażenie 9: 3 = 3. Jeśli w tym wyrażeniu dywidenda i dzielnik zostaną pomnożone lub podzielone przez tę samą liczbę, wówczas iloraz 3 nie ulegnie zmianie.

Pomnóżmy dzielną i dzielnik przez 2 i zobaczmy, co z tego wyjdzie:

(9 × 2): (3 × 2) = 18: 6 = 3

Jak widać na przykładzie, iloraz się nie zmienił.

To samo dzieje się, gdy przesuwamy przecinek w dzielnej i dzielniku. W poprzednim przykładzie, gdzie podzieliliśmy 5,91 przez 1,7, przesunęliśmy przecinek w dzielnej i dzielniku o jedną cyfrę w prawo. Po przesunięciu przecinka ułamek 5,91 został przekształcony na ułamek 59,1, a ułamek 1,7 na zwykłą liczbę 17.

W rzeczywistości w tym procesie nastąpiło pomnożenie przez 10. Tak to wyglądało:

5,91 × 10 = 59,1

Dlatego liczba cyfr po przecinku w dzielniku określa, przez co zostanie pomnożona dywidenda i dzielnik. Innymi słowy, liczba cyfr po przecinku w dzielniku określi, o ile cyfr w dzielnej, a w dzielniku przecinek dziesiętny zostanie przesunięty w prawo.

Dzielenie ułamka dziesiętnego przez 10, 100, 1000

Dzielenie ułamka dziesiętnego przez 10, 100 lub 1000 odbywa się w taki sam sposób jak . Na przykład podziel 2,1 przez 10. Rozwiąż ten przykład, używając narożnika:

Ale jest drugi sposób. Jest lżejszy. Istota tej metody polega na tym, że przecinek w dzielnej przesuwa się w lewo o tyle cyfr, ile jest zer w dzielniku.

Rozwiążmy w ten sposób poprzedni przykład. 2.1: 10. Patrzymy na dzielnik. Interesuje nas, ile jest w nim zer. Widzimy, że jest jedno zero. Oznacza to, że w dywidendzie 2,1 należy przesunąć przecinek w lewo o jedną cyfrę. Przesuwamy przecinek w lewo o jedną cyfrę i widzimy, że nie ma już więcej cyfr. W takim przypadku dodaj kolejne zero przed liczbą. W rezultacie otrzymujemy 0,21

Spróbujmy podzielić 2,1 przez 100. W 100 są dwa zera. Oznacza to, że w dywidendzie 2.1 musimy przesunąć przecinek w lewo o dwie cyfry:

2,1: 100 = 0,021

Spróbujmy podzielić 2,1 przez 1000. W 1000 są trzy zera. Oznacza to, że w dywidendzie 2.1 należy przesunąć przecinek w lewo o trzy cyfry:

2,1: 1000 = 0,0021

Dzielenie ułamka dziesiętnego przez 0,1, 0,01 i 0,001

Dzielenie ułamka dziesiętnego przez 0,1, 0,01 i 0,001 odbywa się w taki sam sposób jak . W dzielnej i dzielniku należy przesunąć przecinek w prawo o tyle cyfr, ile jest po przecinku w dzielniku.

Na przykład podzielmy 6,3 przez 0,1. Na początek przesuńmy przecinki w dzielnej i dzielniku w prawo o tyle cyfr, ile jest w dzielniku po przecinku. Dzielnik ma jedną cyfrę po przecinku. Oznacza to, że przecinki w dzielnej i dzielniku przesuwamy w prawo o jedną cyfrę.

Po przesunięciu przecinka w prawo o jedną cyfrę, ułamek dziesiętny 6,3 staje się zwykłą liczbą 63, a ułamek dziesiętny 0,1 po przesunięciu przecinka w prawo o jedną cyfrę zamienia się w jeden. A dzielenie 63 przez 1 jest bardzo proste:

Oznacza to, że wartość wyrażenia 6,3: 0,1 wynosi 63

Ale jest drugi sposób. Jest lżejszy. Istota tej metody polega na tym, że przecinek w dzielnej przesuwa się w prawo o tyle cyfr, ile jest zer w dzielniku.

Rozwiążmy w ten sposób poprzedni przykład. 6,3: 0,1. Spójrzmy na dzielnik. Interesuje nas, ile jest w nim zer. Widzimy, że jest jedno zero. Oznacza to, że w dywidendzie 6,3 należy przesunąć przecinek w prawo o jedną cyfrę. Przesuń przecinek w prawo o jedną cyfrę i uzyskaj 63

Spróbujmy podzielić 6,3 przez 0,01. Dzielnik liczby 0,01 ma dwa zera. Oznacza to, że w dywidendzie 6,3 musimy przesunąć przecinek w prawo o dwie cyfry. Ale w dywidendzie jest tylko jedna cyfra po przecinku. W takim przypadku musisz dodać kolejne zero na końcu. W rezultacie otrzymujemy 630

Spróbujmy podzielić 6,3 przez 0,001. Dzielnik liczby 0,001 ma trzy zera. Oznacza to, że w dywidendzie 6,3 musimy przesunąć przecinek w prawo o trzy cyfry:

6,3: 0,001 = 6300

Zadania do samodzielnego rozwiązania

Czy podobała Ci się lekcja?
Dołącz do nas nowa grupa VKontakte i zacznij otrzymywać powiadomienia o nowych lekcjach

Ułamki

Uwaga!
Są dodatkowe
materiały w sekcji specjalnej 555.
Dla tych, którzy są bardzo „nie bardzo…”
A dla tych, którzy „bardzo…”)

W szkole średniej ułamki nie są zbyt uciążliwe. Na razie. Dopóki nie natkniesz się na potęgi z wymiernymi wykładnikami i logarytmami. A tam... Naciskasz i naciskasz kalkulator, a pojawia się pełny wyświetlacz niektórych liczb. Trzeba myśleć głową jak w trzeciej klasie.

W końcu wymyślmy ułamki! No, ile można się w nich pogubić!? Co więcej, wszystko jest proste i logiczne. Więc, jakie są rodzaje ułamków?

Rodzaje ułamków. Transformacje.

Są ułamki trzy typy.

1. Ułamki zwykłe , Na przykład:

Czasami zamiast poziomej linii wstawia się ukośnik: 1/2, 3/4, 19/5, cóż, i tak dalej. Tutaj często będziemy używać tej pisowni. Wybierany jest najwyższy numer licznik ułamka, niżej - mianownik. Jeśli ciągle mylicie te nazwy (zdarza się...), powiedzcie sobie zdanie: „ Zzzzz Pamiętać! Zzzzz mianownik - spójrz zzzzz uh!” Słuchaj, wszystko zostanie zapamiętane.)

Kreska, pozioma lub nachylona, ​​oznacza dział od góry (licznik) do dołu (mianownik). To wszystko! Zamiast myślnika całkiem możliwe jest umieszczenie znaku podziału - dwóch kropek.

Jeżeli możliwy jest całkowity podział, należy tego dokonać. Zatem zamiast ułamka „32/8” znacznie przyjemniej jest napisać liczbę „4”. Te. 32 dzieli się po prostu przez 8.

32/8 = 32: 8 = 4

O ułamku „4/1” nawet nie mówię. Co również jest po prostu „4”. A jeśli nie jest to całkowicie podzielne, zostawiamy to jako ułamek. Czasami trzeba wykonać operację odwrotną. Zamień liczbę całkowitą na ułamek. Ale o tym później.

2. Dziesiętne , Na przykład:

W tej formie będziesz musiał zapisać odpowiedzi na zadania „B”.

3. Liczby mieszane , Na przykład:

Liczby mieszane praktycznie nie są używane w szkole średniej. Aby z nimi pracować, należy je przekształcić w zwykłe ułamki. Ale na pewno musisz to umieć! Inaczej natkniesz się na taki numer w problemie i zamarzniesz... Znikąd. Ale będziemy pamiętać tę procedurę! Trochę niżej.

Najbardziej wszechstronny ułamki zwykłe. Zacznijmy od nich. Nawiasem mówiąc, jeśli ułamek zawiera wszelkiego rodzaju logarytmy, sinusy i inne litery, niczego to nie zmienia. W tym sensie, że wszystko działania z wyrażeniami ułamkowymi nie różnią się od działań ze zwykłymi ułamkami!

Główna właściwość ułamka.

Więc chodźmy! Na początek cię zaskoczę. Cała gama przekształceń ułamkowych zapewniana jest przez jedną właściwość! Tak to się nazywa główna właściwość ułamka. Pamiętać: Jeśli licznik i mianownik ułamka zostaną pomnożone (podzielone) przez tę samą liczbę, ułamek się nie zmieni. Te:

Oczywiste jest, że możesz pisać dalej, aż zsiniejesz na twarzy. Nie pozwól, aby sinusy i logarytmy Cię zmyliły, zajmiemy się nimi dalej. Najważniejsze jest, aby zrozumieć, że wszystkie te różne wyrażenia są ten sam ułamek . 2/3.

Czy tego potrzebujemy, tych wszystkich przemian? Tak! Teraz przekonasz się sam. Na początek skorzystajmy z podstawowej właściwości ułamka dla ułamki redukujące. Wydawałoby się, że to elementarna rzecz. Podziel licznik i mianownik przez tę samą liczbę i gotowe! Nie da się popełnić błędu! Ale... człowiek jest istotą twórczą. Wszędzie możesz popełnić błąd! Zwłaszcza jeśli musisz zmniejszyć nie ułamek taki jak 5/10, ale wyrażenie ułamkowe z różnymi rodzajami liter.

Jak poprawnie i szybko redukować ułamki bez wykonywania dodatkowej pracy, można przeczytać w specjalnym rozdziale 555.

Zwykły uczeń nie zawraca sobie głowy dzieleniem licznika i mianownika przez tę samą liczbę (lub wyrażenie)! Po prostu przekreśla wszystko, co jest takie samo powyżej i poniżej! To tutaj się czai typowy błąd, wpadka, jeśli wolisz.

Na przykład musisz uprościć wyrażenie:

Tu nie ma o czym myśleć, przekreśl literę „a” na górze i „2” na dole! Otrzymujemy:

Wszystko jest poprawne. Ale tak naprawdę podzieliliście się Wszystko licznik i Wszystko mianownikiem jest „a”. Jeśli jesteś przyzwyczajony do po prostu przekreślania, możesz w pośpiechu skreślić „a” w wyrażeniu

i zdobądź to jeszcze raz

Co byłoby kategoryczną nieprawdą. Ponieważ tutaj Wszystko licznik na „a” już jest nie udostępnia! Ułamka tego nie można zmniejszyć. Swoją drogą taka obniżka to... hmm... poważne wyzwanie dla nauczyciela. Tego się nie wybacza! pamiętasz? Redukując, musisz dzielić Wszystko licznik i Wszystko mianownik!

Zmniejszanie ułamków znacznie ułatwia życie. Dostaniesz gdzieś ułamek, na przykład 375/1000. Jak mogę teraz kontynuować z nią współpracę? Bez kalkulatora? Pomnóż, powiedz, dodaj, podnieś do kwadratu!? A jeśli nie jesteś zbyt leniwy, to ostrożnie skróć go o pięć, a potem o kolejne pięć, a nawet… krótko mówiąc, w trakcie skracania. Zdobądźmy 3/8! Dużo ładniej, prawda?

Główna właściwość ułamka pozwala na konwersję zwykłych ułamków zwykłych na dziesiętne i odwrotnie bez kalkulatora! To ważne dla ujednoliconego egzaminu państwowego, prawda?

Jak zamienić ułamki jednego typu na inny.

W przypadku ułamków dziesiętnych wszystko jest proste. Jak się słyszy, tak jest napisane! Powiedzmy 0,25. To jest zero przecinek dwadzieścia pięć setnych. Piszemy więc: 25/100. Zmniejszamy (dzielimy licznik i mianownik przez 25), otrzymujemy zwykły ułamek: 1/4. Wszystko. To się zdarza i nic nie zostaje zredukowane. Jak 0,3. To trzy dziesiąte, tj. 3/10.

A co jeśli liczby całkowite nie są zerem? Jest w porządku. Zapisujemy cały ułamek bez przecinków w liczniku i mianowniku - co słychać. Na przykład: 3.17. To jest trzy przecinek siedemnaście setnych. W liczniku zapisujemy 317, a w mianowniku 100. Otrzymujemy 317/100. Nic nie jest redukowane, to znaczy wszystko. To jest odpowiedź. Elementarne, Watsonie! Z tego wszystkiego, co zostało powiedziane, użyteczny wniosek: każdy ułamek dziesiętny można zamienić na ułamek zwykły .

Ale niektórzy ludzie nie mogą dokonać odwrotnej konwersji ze zwykłego na dziesiętny bez kalkulatora. I jest to konieczne! Jak zapiszesz odpowiedź na egzaminie Unified State Exam!? Przeczytaj uważnie i opanuj ten proces.

Jaka jest cecha ułamka dziesiętnego? Jej mianownik to Zawsze kosztuje 10, 100, 1000 lub 10000 i tak dalej. Jeśli twój ułamek zwykły ma taki mianownik, nie ma problemu. Na przykład 4/10 = 0,4. Lub 7/100 = 0,07. Lub 12/10 = 1,2. A co by było, gdyby odpowiedź na zadanie z sekcji „B” okazała się 1/2? Co napiszemy w odpowiedzi? Wymagane są ułamki dziesiętne...

Pamiętajmy główna właściwość ułamka ! Matematyka korzystnie pozwala pomnożyć licznik i mianownik przez tę samą liczbę. Swoją drogą, cokolwiek! Oprócz zera, oczywiście. Wykorzystajmy więc tę właściwość na naszą korzyść! Przez co można pomnożyć mianownik, tj. 2, aby uzyskać liczbę 10, 100 lub 1000 (oczywiście im mniej, tym lepiej...)? Oczywiście o 5. Możesz pomnożyć mianownik (tzn nas konieczne) przez 5. Ale wtedy licznik należy również pomnożyć przez 5. To już jest matematykażąda! Otrzymujemy 1/2 = 1x5/2x5 = 5/10 = 0,5. To wszystko.

Jednak spotykają się różne mianowniki. Możesz natknąć się na przykład na ułamek 3/16. Spróbuj dowiedzieć się, przez co pomnożyć 16, aby otrzymać 100 lub 1000... Czy to nie działa? Wtedy możesz po prostu podzielić 3 przez 16. W przypadku braku kalkulatora będziesz musiał podzielić rogiem na kartce papieru, jak w klasy młodsze nauczał. Otrzymujemy 0,1875.

Są też bardzo złe mianowniki. Na przykład nie ma możliwości zamiany ułamka 1/3 na dobry ułamek dziesiętny. Zarówno na kalkulatorze, jak i na kartce papieru otrzymujemy 0,3333333... Oznacza to, że 1/3 to dokładny ułamek dziesiętny nie przetłumaczone. To samo co 1/7, 5/6 i tak dalej. Jest ich wiele, nieprzetłumaczalnych. To prowadzi nas do kolejnego przydatnego wniosku. Nie każdy ułamek zwykły można zamienić na ułamek dziesiętny !

Swoją drogą, to przydatne informacje do samodzielnego testu. W części „B” należy wpisać ułamek dziesiętny w swojej odpowiedzi. I masz na przykład 4/3. Ułamek ten nie jest konwertowany na ułamek dziesiętny. Oznacza to, że gdzieś po drodze popełniłeś błąd! Wróć i sprawdź rozwiązanie.

Więc wymyśliliśmy ułamki zwykłe i dziesiętne. Pozostaje poradzić sobie z liczbami mieszanymi. Aby z nimi pracować, należy je przekształcić w zwykłe ułamki. Jak to zrobić? Możesz złapać szóstoklasistę i go zapytać. Ale szóstoklasista nie zawsze będzie pod ręką... Musisz to zrobić sam. To nie jest trudne. Musisz pomnożyć mianownik części ułamkowej przez część całkowitą i dodać licznik części ułamkowej. Będzie to licznik ułamka zwykłego. A co z mianownikiem? Mianownik pozostanie taki sam. Brzmi skomplikowanie, ale w rzeczywistości wszystko jest proste. Spójrzmy na przykład.

Załóżmy, że przestraszyłeś się, widząc liczbę związaną z problemem:

Myślimy, że spokojnie, bez paniki. Cała część to 1. Jednostka. Część ułamkowa to 3/7. Dlatego mianownik części ułamkowej wynosi 7. Mianownik ten będzie mianownikiem ułamka zwykłego. Liczymy licznik. Mnożymy 7 przez 1 (część całkowitą) i dodajemy 3 (licznik części ułamkowej). Otrzymujemy 10. Będzie to licznik ułamka zwykłego. To wszystko. W zapisie matematycznym wygląda to jeszcze prościej:

Czy to jasne? Zatem zapewnij sobie sukces! Zamień na ułamki zwykłe. Powinieneś dostać 10/7, 7/2, 23/10 i 21/4.

W szkole średniej rzadko wymagana jest operacja odwrotna – zamiana ułamka niewłaściwego na liczbę mieszaną. Cóż, jeśli tak... A jeśli nie jesteś w szkole średniej, możesz zapoznać się ze specjalną sekcją 555. Nawiasem mówiąc, około ułamki niewłaściwe dowiesz się.

No cóż, to praktycznie wszystko. Zapamiętałeś rodzaje ułamków i zrozumiałeś Jak przenieść je z jednego typu na drugi. Pozostaje pytanie: Po co zrobić to? Gdzie i kiedy zastosować tę głęboką wiedzę?

odpowiadam. Każdy przykład sam w sobie sugeruje niezbędne działania. Jeśli w przykładzie zmieszamy ułamki zwykłe, dziesiętne, a nawet liczby mieszane, wszystko zamienimy na ułamki zwykłe. Zawsze można to zrobić. Cóż, jeśli jest napisane coś w rodzaju 0,8 + 0,3, to liczymy to w ten sposób, bez żadnego tłumaczenia. Dlaczego potrzebujemy dodatkowa praca? Wybieramy rozwiązanie, które jest wygodne nas !

Jeśli zadaniem są same ułamki dziesiętne, ale... jakieś złe, przejdź do zwykłych i spróbuj! Słuchaj, wszystko się ułoży. Na przykład będziesz musiał podnieść do kwadratu liczbę 0,125. To nie jest takie proste, jeśli nie przyzwyczaiłeś się do korzystania z kalkulatora! Nie tylko musisz pomnożyć liczby w kolumnie, ale także pomyśleć o tym, gdzie wstawić przecinek! Na pewno nie będzie to działać w Twojej głowie! A co jeśli przejdziemy do ułamka zwykłego?

0,125 = 125/1000. Zmniejszamy go o 5 (to na początek). Dostajemy 25/200. Znowu o 5. Dostajemy 5/40. Och, wciąż się kurczy! Powrót do 5! Dostajemy 1/8. Możemy to łatwo wyrównać (w naszych umysłach!) i uzyskać 1/64. Wszystko!

Podsumujmy tę lekcję.

1. Istnieją trzy rodzaje ułamków. Liczby zwykłe, dziesiętne i mieszane.

2. Liczby dziesiętne i mieszane Zawsze można zamienić na ułamki zwykłe. Przeniesienie zwrotne nie zawsze możliwy

3. Wybór rodzaju ułamków do pracy z zadaniem zależy od samego zadania. W zależności od dostępności różne typy ułamki w jednym zadaniu, najbardziej niezawodne jest przejście do ułamków zwykłych.

Teraz możesz ćwiczyć. Najpierw zamień te ułamki dziesiętne na ułamki zwykłe:

3,8; 0,75; 0,15; 1,4; 0,725; 0,012

Powinieneś otrzymać takie odpowiedzi (w bałaganie!):

Zakończmy to. Na tej lekcji odświeżyliśmy naszą pamięć kluczowe punkty przez ułamki. Zdarza się jednak, że nie ma nic specjalnego do odświeżenia...) Jeśli ktoś zupełnie o tym zapomniał, albo jeszcze tego nie opanował... Wtedy można przejść do specjalnego Sekcji 555. Wszystkie podstawy są tam szczegółowo omówione. Wielu nagle wszystko zrozumieć zaczynają się. I rozwiązują ułamki na bieżąco).

Jeśli podoba Ci się ta strona...

Przy okazji, mam dla Ciebie jeszcze kilka ciekawych stron.)

Możesz poćwiczyć rozwiązywanie przykładów i sprawdzić swój poziom. Testowanie z natychmiastową weryfikacją. Uczmy się - z zainteresowaniem!)

Można zapoznać się z funkcjami i pochodnymi.